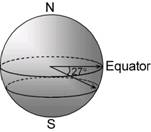
Using latitude and longitude, you can describe any position on the surface of the Earth. First up, you need to describe what latitude a position is at, by specifying which parallel of latitude the position is located on. For instance, Brisbane is about 27 degrees south of the equator. What this means is shown in this diagram:
Sponsored Links
The 27 degrees indicates how far ‘up’ or ‘down’ the globe the parallel of latitude is. In this case, because it’s 27 degrees south, we go downwards from the equator. Now, specifying only the latitude isn’t enough to pinpoint a location on the globe. We could be talking about any point on this circle of latitude. Brisbane has a longitude of “153 degrees east”. The angle of longitude lines are measured relative to the longitude line that passes through Greenwich, in England. Other longitudes are specified by how many degrees east or west of this line they are. So the Brisbane longitude is:
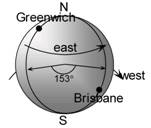
I’ve shown the directions that going east and west from Greenwich are in this diagram.
If you put these two things together, you’ll get the intersection point of a line of latitude and a line of longitude that pinpoints the position you’re talking about:
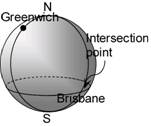
The formal way to specify this position is:
(27° S 153° E)
Finding distances along meridians of longitude
You can use your knowledge of circle arcs to work out the distances between two points that lie on the same meridian of longitude. For instance, say we wanted to find the distance along the surface of the Earth between point A and point B:
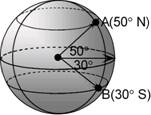
First of all, from looking at the diagram we can see that both A and B lie on the same meridian of longitude. This meridian of longitude is just one big circle that goes all the way around the Earth in the vertical direction, passing through both poles. The part of it between points A and B is just an arc. To work out the length of any arc, all we need to know is the radius of the circle, and the angle of the arc.
The radius of the Earth is one of those common knowledge things. It’s about 6,378 km. Because the Earth spins, it’s actually not quite a perfect sphere; it’s a bit bloated in the middle because of the spinning movement. But 6,378 km is fine for most calculations.
The angle of the arc we can work out by starting at point A and moving down to point B. Moving from point A to the equator of the Earth, we’ve travelled 50 degrees. Then, moving from the equator down to point B, we’ve travelled another 30 degrees. This adds to a total of 80 degrees. So the distance we’re trying to calculate is for an 80 degree arc, which is part of a circle with a radius of 6,378 km.

We can use the arc length formula to work out how long our arc is:
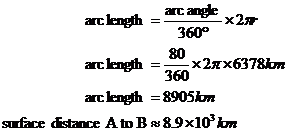
Finding distances along parallels of latitude
Meridians of longitude are all the same size circles. Parallels of latitude on the other hand are different sized circles, depending on what latitude the circle is at. The biggest one is the latitude line at the equator, and they get progressively smaller as you head either north or south from there.
Finding the distance between two points on the same parallel of latitude is a two step process. For instance, we might be trying to find the distance between C and D in this diagram:

C and D are on the same parallel of latitude. C is 57° west of the longitude line which passes through Greenwich, which has a longitude of 0°. D is 35° east of the 0° longitude line. So we know that the arc between them takes up a total of 92° of the circle that is their parallel of latitude. Here’s that circle by itself:
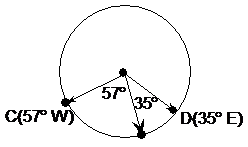
However, we don’t know the radius of this circle. The only parallel of latitude circle that has a radius the same as the Earth’s is the latitude line at the equator. All the other latitude circles have radii smaller than the Earth’s radius. We can work out the radius of our particular circle by using the diagram. Notice how our parallel of latitude is 30° south of the equator. There is a right angled triangle you can form between the centre of the Earth, the centre of our circle of latitude, and any point on the circumference of our circle of latitude. In the diagram this triangle is shown by thick white lines:
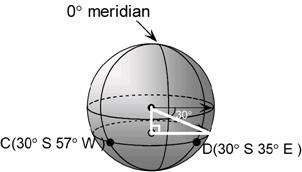
The hypotenuse of this triangle is the radius of the Earth, since it goes all the way from the Earth’s centre to the surface. The middle length side is the radius of our circle of latitude, which is what we’re trying to find. We can also work out an angle inside the triangle, since we know the 30° angle just outside it:

The 60 degree angle can be worked out because we know it and the 30 degree angle need to add to a right angle. The 30 degree angle in the triangle can be worked out by remembering the ‘Z’ formed by the two parallel lines, or by remembering that interior angles in a triangle add to 180°.
We can now just use cosine to find out what the radius of our circle of latitude is:

With the radius of our latitude circle known now, we can work out the length of the arc between C and D:

Notice that we get very similar answers for this latitude example and the previous longitude answer, even though the arc angle in this case is 12° larger. This time however the circle’s radius was smaller, which sort of cancels out against the bigger angle to give a very similar answer.

