Rolling circle

Lots of things can be made to roll along the ground.  For instance, think about a tyre on a car rolling along the ground.  If you had to trace out the locus for a point on the tyre as it rolled along the ground, what would it look like?

 

Well, first of all, we know that point A can’t get any lower cause it’s at ground level.  What we can do is draw the wheel several times as it rolls to the right, and show where point A is going to be at each time.  For a start, let’s draw the tyre a little later in time and work out where point A is going to be:

So the lighter shaded wheel shows the tyre at the start, and the darker shaded wheel shows it after it’s rolled a little bit.  The straight line with arrowheads underneath the ground shows how far the tyre has rolled.  This distance is the same as the distance around the tyre that point A has moved, shown by the curved line with the arrowhead.  We can do this procedure over and over again, like this:

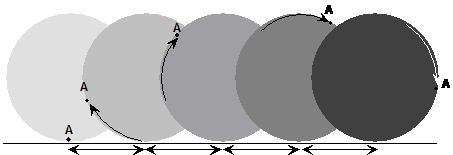
To draw the locus, all you need to do is draw a line through the A points at each time interval, like this:

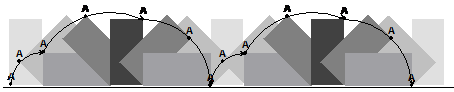
Now, because it’s a rolling object, we really need to show a couple of complete cycles.  One cycle is when point A gets back to where it started, in this case touching the ground.  You can do this by drawing even more tyre configurations; you should end up with a trajectory that looks like this:

These shapes are known as cycloids.  Their formal definition is:

A cycloid is the locus for the point on the rim of a circle rolling along a straight line.

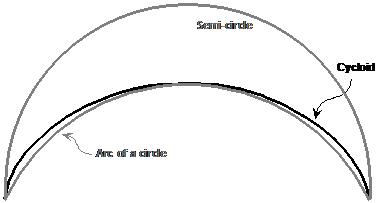
Note that although it looks very much like part of a circle, it actually has different shape to a circle arc and a semi-circle, as shown in this diagram:

Rolling square

Although it’s not a shape you’d find as the tyre of a car, there are situations where you might see a square shape being ‘rolled’ along the ground.  For instance, if there was a heavy box with square ends on the ground, and it was too heavy to lift – someone might sort of roll it along instead.  Once again, to draw the locus, you need to draw the square at different times as it rolls along the ground and follow a point on it.  Shapes with corners roll differently to circles – they pivot on the corners as they roll:

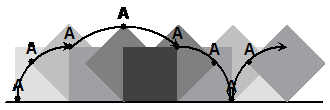
When the square pivots on its bottom right corner at the start, point A is tracing out part of a circle with a radius equal to the side length of the square.  In the next part of the sequence, because point A is the diagonal length of the square away from the pivot point, it traces out part of a bigger circle with a radius equal to the diagonal length of the square.

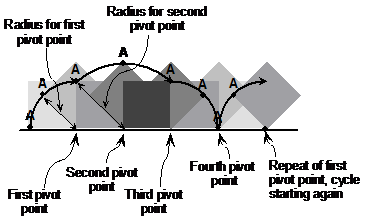
Notice that when the point A itself is the pivot point, it doesn’t move as the square rolls through 90°.  In the diagram, point A is the pivot point at the fourth pivot point, and doesn’t actually move as the square pivots around it.  It only starts moving again when the pivot point changes back to the first pivot point again.

A rectangle rolling is a little more complicated.  You can work out the locus the same way, but it takes a little longer.  Also, because it’s not a square, the circular segments don’t start and stop as neatly as they do for the square.