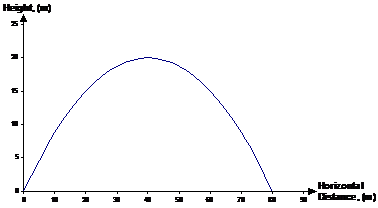
This locus is for any situation where you shoot or throw something at an angle into the air. Things like throwing a tennis ball to a friend, or shooting a gun, or throwing a javelin. The shape of the locus for a situation like this is a parabola, like this one for a thrown cricket ball:
Sponsored Links
This graph shows the trajectory of the ball as if you were looking at it from the side from a long way away. The horizontal axis shows how far the ball has travelled in the horizontal direction from the person who threw it, and the vertical axis shows how high the ball gets in the vertical direction above the ground. Notice that the ball starts 0 metres above the ground, if we were being really accurate we’d have to start it at about 1.5 metres above the ground, representing the fact that it starts in the person’s hand rather than actually on the ground.
Projectile locus with air resistance
If you’ve ever stuck your hand outside the car window when you’ve been on a highway going 100 km/hr, you would have noticed that there was a pretty strong ‘wind’ blowing on your hand. This ‘wind’ is air resistance – as you move through air, it ‘resists’ you travelling through it. When you’re just walking, you don’t really notice it, because you’re moving so slowly. Air resistance is generally proportional to the square of your speed. So if you double how fast you’re travelling, you quadruple the air resistance you’d feel. The graph above shows what the trajectory would be like if the cricket ball had been thrown somewhere in a vacuum (where there is no air), such as on the surface of the moon. Of course then the ball would have gone a lot further because gravity is weaker on the moon, but that’s another kettle of fish.
This air resistance makes the locus for a thrown cricket ball look a little bit different.
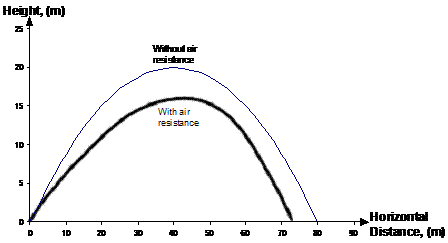
To calculate the exact shape of the trajectory or locus is quite a complicated thing to do and requires high level mathematics. The shape of the projectile, whether it’s thrown with any spin on it and a whole heap of other factors affect exactly how it would move through the air. But the trajectory shown in this second graph should give you a general idea – the ball doesn’t go quite as far, or as high. Also, the last part of its trajectory when the ball is going downwards is a lot steeper than when the ball is initially going upwards.

