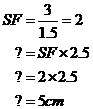Similar figures and geometric constructions

Similar figures are the same shape as each other, but may be different sizes.  The scale factor is the ratio between the sizes of the two shapes.  For instance, these two similar rectangles have a scale factor of 2.0:

The scale factor is the ratio between the lengths of any corresponding sides.  For instance, we could work the scale factor out by comparing the top side lengths – one is 2.5 cm long, and one is 5 cm long, twice as long.  The scale factor does not correspond to the ratio in the areas of the two shapes.  These rectangles have a scale factor of 2, but the ratio between their areas is 4.

In general, if you’re trying to work out the scale factor, find two corresponding sides and work out the ratio in their side lengths.  You can’t use angles to work out a scale factor because the angles don’t change between two similar figures, only the side lengths.

Say we didn’t know the length of the 5 cm side in the large rectangle.  If we were told that the rectangles were similar, we could first work out the scale factor using the 1.5 cm and 3 cm sides.  Then, we could multiply the 2.5 cm side on the small rectangle by the scale factor to work out the length of the unknown side in the large rectangle.