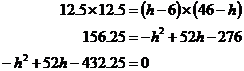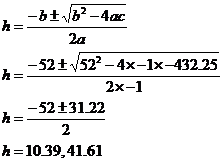Circle geometry
A circle is a very special type of shape, and you will most likely encounter a lot of questions about them. Apart from working out their area and circumference, there are a lot of questions which you can only answer if you know the special properties that circles have regarding angles, chords etc…
Circle tangent lines
The tangent is a straight line that just touches a curved surface, and is exactly parallel to the curved surface at the touching point. In a circle, any tangent drawn on the outside circumference is perpendicular to a radius line drawn from the circle’s centre to the tangent contact point:
Sponsored Links

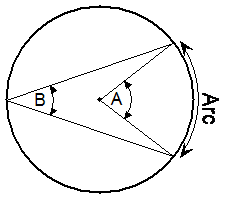
Arc angles
![]()
An arc is a segment of the outside circumference of a circle. Normally when you talk about the arc angle, you’re talking about angle ‘A’ in the diagram above – the angle between the two radius lines that touch either end of the arc. However, you can also talk about angle B, which is the angle the arc subtends at the circumference. ‘Subtends’ means that something is opposite to something else, and also defines the limits of that other thing. For instance, the arc subtends angle B because it is opposite angle B, and also defines how far angle B reaches in either direction.
You can prove that ![]() by realising that four parts of the
shape formed inside the circle are the same length – the radius length sides:
by realising that four parts of the
shape formed inside the circle are the same length – the radius length sides:
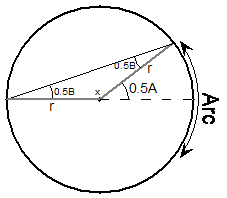
Since the circle is a mirror image vertically, I’ve only drawn in the top half of the interior shape. The two sides which are the radii are labelled ‘r’. I’ve also labelled the new ‘half’ angles. This triangle is an isosceles triangle because two of its sides are the same length. Because it’s an isosceles triangle, I know that the two small angles are going to be the same size – they’ll both be ‘0.5B’. I’ve also labelled the unknown angle inside the triangle as ‘x’.
Once I’ve done all this, I can write a statement about the angles needing to add up to 180° inside the triangle. I can also write another maths statement saying that the angles forming the straight angle (180°) at the centre of the circle need to add to 180°.
First, the triangle angles:
![]()
And then the angles forming the straight angle:
![]()
We have two equations and three unknowns – A, B and x. This means we can’t find out the values of any of the unknowns. But is this what we want? No! All we want is the relationship between A and B. So all we need to do is eliminate x from the equations. We can do this by rearranging the second equation in terms of x, and then substituting back into the first equation:
![]()
Substitute for x into the first equation:
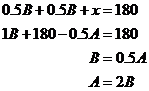
Chord multiplication
A chord is a straight line inside a circle from one point on the circumference to another. There’s a peculiar property for two chords that intersect each other. When they intersect, each chord is split into two lengths. The product of the lengths for one chord is equal to the product of the two lengths for the other chord:
![]()
Angles for the same arc
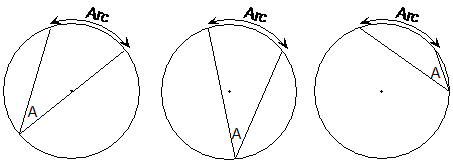
When you have an arc in a circle, you can create an angle with the arc from any point on the circumference apart from the arc bit. Wherever you form the angle from, it will always be the same size for the same arc:
|
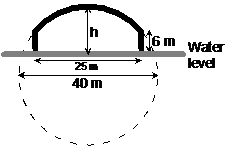
One of the things civil engineers need to do is build bridges. A lot of bridges have an arch like structure. The bridge in the foreground of this picture is in Rome, and has three separate arch bits. Each arch is part of a circle that has a 40 metre diameter. The height from the water to the bottom of the arch along each pylon is 6 metres. Each arch covers a distance of 25 metres of water. How high is the centre of each arch above the water?
|
|
Solution |
|
First up, we need a diagram which just has the essential information in it, with no distractions. We can extend the arch into a full circle shown by the dashed line:
We want to find what ‘h’ is. Now this question is more about lengths than angles, so we need to think about what special properties of circles we know that involve lengths. One we do know is the chord length multiplication property. To use this property, we’re going to need two intersection chords, one of which has to have ‘h’ as part of it, since that’s what we’re trying to find. We can construct two intersecting chords by not thinking about ‘h’, but instead, the height of the arch bit only, not including the height of the pylons which are 6 metres tall. The height of the arch only is going to be ‘h – 6’ metres:
Now we have two intersecting chords – the 25 metre long chord between the ends of the arch, and the vertical chord through the centre of the circle. We know that the vertical chord’s total length is going to be the diameter of the circle, so we can work out the length of ‘x’: So how are the chords split up? Well, the 25 metre chord is split into 2 equal 12.5 metre long segments. The vertical chord is split into a ‘h – 6’ long segment, and a ‘x’ long segment, which we just worked out is ‘46 – h’ long. We know that the products of the two lengths in each segment are equal: With some rearranging we get a quadratic equation, which we can solve using the quadratic formula: Only one answer makes physical sense – the 10.39 metre one. ‘h’ can’t be 41.61 metres above the water because 41.61 metres is larger than the diameter of the circle the arch is part of! So the top of the arch is 10.39 metres above the water. More of the height of the bridge in this case is in the pylons rather than the arch bit. |