If there’s one reason it’s good to learn probability, it’s to understand exactly how gambling works, and why you’re just about always going to end up losing money in the long term. 

Expected returns

One way you can analyse a lot of simple gambling games is by looking at the expected return from one go at the game.  The formula for working this out is:

                                 

The payout is the amount of money the casino gives you if you win, on top of them returning the money you bet.  It does not include the money you bet.  Other names for the expected return are the net profit or earnings, or net gain.

Let’s take a game of Roulette as an example.  Roulette is a simple game involving a wheel which has 37 slots around its middle.  Each slot is numbered from 0 to 36 (yes that makes 37 numbers in total).  Also the slots have colours, usually the ‘0’ slot is coloured uniquely, say green, and then half of the other slots are red, and half are black.   The wheel is spun, and a small ball is thrown on top of it.  Gradually, the wheel slows down, until it stops and the ball ends up in one of the slots.  People bet on where the ball ends up.

Two of the simplest bets are betting on what colour the ball will land on, and what number it will land on.  Here is the information on the payouts for winning:

This means for instance if we bet $10 on the ball landing on red, and it does, we’ll get a payout of $10 from the casino on top of them returning the money we bet.  So all up we’ll get $20 back, of which $10 will be the amount we bet.

There are lots of slight variations on the game, but this will do for the purposes of explaining how it works.  Now, let’s calculate our expected returns or payouts for these types of bets.  We’ll use a bet amount of $1.00.  First, let’s calculate the expected return if we bet that the ball is going to land on a red slot. 

Apart from the ‘0’ slot, half of the other slots are red.  This means there are 18 slots that are red.  Assuming that the ball has an equal chance of ending up in any slot, this means the probability of the ball ending up in a red slot is:

                                           

Now, you can either win, or lose – they are mutually exclusive events.  This means their probabilities add to 1.  So:

                                        

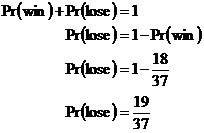
The payout amount that we’ll win if the ball does land on red is the same as what we bet – $1.  Remember the bet amount itself is also $1.

With this information, we can now calculate the expected return:

                                 

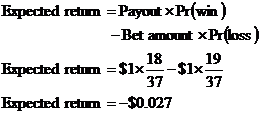
Notice how our expected return is negative.  Think about what this means – the amount of money we expect to earn each time we bet is negative.  This means that on average I’m not going to get any money back, the negative sign means I’ll lose that amount to the casino per bet on average.

Expected isn’t the same as being certain – if we were really lucky we might win money 4 or 5 times in a row betting on red.  But vice versa, we could lose money 4 or 5 times in a row too.  And this expected return tells us that on average, we’re going to lose money in the long run.

What about if we bet on the ball landing on a specific number?  The payout is very big for this – 35 times the bet amount.  So for a $1 bet, the payout is $35.  The probability of winning is a lot lower though – we’re betting on the ball landing on one certain slot out of the 37:

                                                      

This means that:

                                                

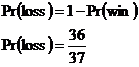
Using our expected return formula:

                                 

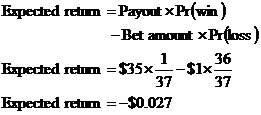
Turns out our expected return is exactly the same as for betting on a colour.  So either way, over the long term, we’re going to lose money.

Other types of Roulette bets

There are other types of bets you can make apart from this simple one.  For instance, you can usually do a six number bet, which pays back five to one.  A “five to one” pay back means that the payout by the casino is fives time as much as you bet, and you also get your bet amount back as well.  In this bet, you get to pick six different numbers – if the ball ends up on any of the six numbers you’ll win.  So for a $1 bet, the payout is $5.  The probability of winning is 6 divided by 37.  The probability of losing is 1 minus the probability of winning, or 31 divided by 37:

                                 

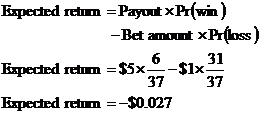
Surprise, surprise – you’re still going to lose over the long term.  Same expected return as for the previous bet types.

Gambler’s ruin

For decades and decades, thousands and thousands of people have tried to get rich from gambling.  Some of these people have been very intelligent, but a lot have been rather lacking in the cranial capacity.  A very, very, very, very, very small number of people have managed to make a small fortune from gambling and then stop.  No-one can gamble at a casino year after year and come out ahead after many decades of gambling, with the exception of some games where if you’re very very very very good and you’ve got a lot of money to start with, you can make a very very very very small amount of money.  And in those cases you’d be much better off putting the money in the bank and then finding something better to do with your time.

Gambler’s ruin is a term used to describe how when you are gambling in a casino, you’re going to lose in the long run no matter what.  There are two main reasons why this is so:

·         Just about all of the games at the casino have negative returns – if you bet money on them, on average you’re going to lose money.

·         The casino has a lot more money to play with than you do.  You may have $10,000 to spend, but a large casino may have a few hundred million dollars.  In the short term, they can afford to lose a lot more money than you can.

Now, let’s think about a gambling game with even odds, which is better than you’ll get at a casino.  The game involves tossing a coin up in the air and betting on what face comes up.  If it comes up heads, you win, if it comes up tails the house (casino) wins.  So if you bet $1 each time, when you win, you’ll get a payout of $1, plus the return of your $1 bet.  If you lose, you’ll lose your $1 bet.

Let’s say that you are gambling your entire fortune away – you’ve got $100,000 to play with.  Let’s also say the casino is a very small one, and only has $1,000,000 of money in reserve.  Because the game you’re playing has even odds, we can plot a graph of how your total amount of money might vary as you played more and more games.  We could also plot a graph for the casino’s total money:

The graph on the left shows my fortune, which starts at $100,000.  It goes up for a while, but then happens to go down quite a bit, and I dip below my $0 line – I’ve gone bankrupt and run out of money.

Now look at the graph showing the bank’s fortune.  They started at $1,000,000.  When I started winning money, they lost money, but me winning doesn’t make anywhere near as much of a dent on their fortune, since they’ve got a lot more money to start with.  Then, when I lose for a while and eventually go bankrupt, they end up $100,000 richer.

This is why the casino will win eventually, even with a game that has even odds.  As you play the game, your fortune will vary upwards and downwards.  If you play for long enough, it will at some stage dip below the $0 mark and you will go bankrupt. 

For instance, compare these two situations:

The casino wins because it has a large pile of cash which allows it to absorb these short term fluctuations in how much money it has.  People betting money on the other hand have much smaller cash piles, and can’t handle anywhere near as much variation in their fortune, which means they’re going to go bust a long time before the casino.  When that happens, the casino will be richer by however much money they have bet.

Now, this explanation was for a betting game which has even odds.  Most of the games in the casino are rigged so that you have worse than even odds.  This means that the time it takes for your fortune to fluctuate below the $0 mark is going to be even less.

Doubling your bet each time

One other technique people talk about is this one, for a simple game like coin flipping where you get back $2 total if you win with a $1 bet:

·         Bet $1. 

·         If you win, bet $1 more. 

·         If you lose, double your bet amount and bet again. 

·         Repeat until you win.

The basic problem with this plan is that you don’t have an infinite amount of money.  The reason you double your bet amount every time you lose is because you need the bigger payout from a larger bet to cover the money you’ve lost on previous bets.  For instance, say this was a sequence of bets I made:

·         Bet $1 and lost.  $1 down overall.

·         Bet $2 and lost.  $3 down overall.

·         Bet $4 and lost.  $7 down overall.

·         Bet $8 and won. $1 up overall.

The problem is, if you keep doing this technique eventually you’re going to get a long sequence of bets where you don’t win, and you have to double your bet amount.  However there’s a limit to how much you can double your bet amount.  Say you’ve only got $100 to bet.  Then you can’t afford to lose more than 5 bets in a row.  If you do lose six bets in a row, you won’t be able to double your bet for the 7^th game because you don’t have enough money.  And doubling your bet is your only chance for ending up with a profit. 

Sequence of bet amounts in a 6 game losing streak: $1, $2, $4, $8, $16, $32

After 6 losing games, I have used $63 of my money, and I only have $37 left. But in order to double my bet again, I need $64. If you keep using this technique you will eventually get to a stage where you lose too many games in a row, can’t double your bet and end up losing money overall.

Blackjack

Blackjack is a fairly simple card game, where players play “against the house”.  First up, each player chooses how much money to bet.  Each player is then dealt two cards each, face up.  Two cards are also dealt to the ‘house’ (the casino) as well, one face up and one face down.  From now on, the guy running the game goes around each of the players, who can choose to have a card dealt to them if they want.  The aim of the players is to get a total score as close to ‘21’ as possible, without going over, which is known as ‘going bust’.

·         The number cards are worth their number – so a ‘6’ of hearts is worth 6 points.  All the picture cards – the jack, queen and king – are worth 10 pts each.  The ace can be worth one of two different values – 1 or 11.  What it is worth is the player’s decision.

·         Once all the players have decided to stop getting dealt cards, or have gone bust, the dealer (who plays for the casino) turns up the house’s face down card. 

·         Most times the casino will play the game in a very consistent way – if the total of its cards is 16 or less, the dealer will deal another card.  If the total of its cards is 17 or more, it won’t deal any more cards – it will ‘stay’.

·         So each game ends with all the players and the casino either staying on a certain score, or getting over 21 points and going bust.  Players can win in several different ways:

·         If the casino goes bust, then all players who haven’t gone bust yet win a payout equal to their bet amount

·         If the casino doesn’t go bust, then the players with a higher score than the casino win a payout equal to their bet amount.  Getting an equal score to the house means you lose.

·         If the first two cards that are dealt to you are a picture card and an ace, then you have got a ‘blackjack’ – 10 + 11 = 21.  You automatically win a payout equal to one and a half times your bet amount.  The only exception is if the house also gets a ‘blackjack’, in which case you just get your bet amount back.

You lose your bet if any of the following happens:

·         You get a score over 21 and go bust

·         You don’t go bust but end up with a score equal to or lower than the casino’s score.

Blackjack is a very popular game, because the odds aren’t as badly geared against you as for many other gambling games, if you can play it well.  There is a famous basic strategy involving you following a set of rules on how to play.  When you play using basic strategy, on average you’ll lose only about half a percent of how much you bet.  So say I play blackjack all night, starting with $1000, and use basic strategy the whole time.  I should, on average, walk out of the casino with $995 of my money.  I will have made a small loss of $5.  Many players play for the enjoyment and excitement of playing, and are quite happy to pay such a small amount for a night’s worth of entertainment.

Now each casino has its own special rules and variations on the game of blackjack, which means some casinos have slightly better odds than others.  However, even at the friendliest casinos, the odds are slightly against you, so you will lose money even using basic strategy.  However, there is one thing you can do to get a slight edge on the casino:

Card counting

Blackjack games in a casino are usually played with a set of cards made up of several 52 card packs.  Typically, a casino might combine eight 52 card packs together to make a mega pack with 416 cards.  After each game, all the cards that have been dealt in that game are not put back in the pack, they are discarded.  Card counting involves remembering what cards have already been played in previous games.  Since they’ve already been played, this means they won’t show up in future games – this information can be used to tilt the odds fractionally in your favour.

For instance, let’s take a simple case, where you’re playing blackjack at a casino using only one 52 card deck.  You’ve played a couple of games already, and you notice that all the kings, queens and jacks have already been dealt and discarded.  In the current game, you’re sitting on 12 points, and are wondering whether to ask for another card.  You want to get closer to 21 points, but you don’t want to go bust (go over 21 points).  What cards could make you go bust?

Well, only the picture cards, which are all worth 10 pts, could make you go bust – 12 + 10 = 22.  But you know that all the picture cards have already been dealt in previous games and discarded from play.  This means that there is no chance you can get a picture card dealt to you in this current game.  So it’s safe to ask for another card – the numbers 1 to 9 aren’t going to make you go bust, but are going to make you get closer to 21 points, which is a good thing.  The ace can be worth 1 or 11 points – if you get it dealt to you, you just need to specify that it is worth only 1 point, and your score will only go up to 13, which is safe.

Now, of course, when the casino uses eight decks of cards, it becomes a lot harder to remember all the cards that have been dealt.  Also, usually to make life difficult for card counters, the casino will get a brand new set of cards once it has used up half the big pile, rather than playing games until the pile has been completely used up.  By only going till the pile is half used, even if the player remembers all the cards that have been discarded, there is more uncertainty in the player’s mind about what is left in the pile.  If the game was played all the way to the end of the pile, when there were only 10 cards left in the pile a really good card counter would know exactly what those 10 cards were.

Because the odds are so close to even when you play blackjack using basic strategy, all you need is a slight edge in order to tilt the odds in your favour.  Card counting offers this slight edge, and can tip the game in your balance so that on average you are earning a 1% payout on what you bet.  This means that if you bet $1000 each time you play a game, you should on average get back $1010 – a $10 profit per game.  But that’s only on average – what will actually happen is you’ll lose a lot of games, hopefully win a lot of games, and when you add up all your losses and all your profits you’ll end up slightly ahead.  For instance, over a night of games, your earnings / losses might be like this:

This table shows how you might have gone over 20 games of blackjack, betting $1000 each time.  The net return for the first game was $1000, meaning you bet $1000 and won, getting $2000 back, for a net return or profit of $1000.  Looking at the table, in the 7^th game we must have got ‘blackjack’, because the net return was $1500 – 1.5 times the bet amount. In this example the net amount earned for the entire night was $500.

You need capital though

Because the odds are only slightly in your favour, even using card counting, you need to have a fair amount of capital so you can absorb periods of ‘bad luck’.  It’s like flipping a coin – you should get roughly even numbers of ‘heads’ and ‘tails’.  But you never know, you might get 10 heads in a row.  Same with blackjack – even though you’ve got a good strategy and are card counting, you may still lose 10 games in a row.  You need to have a large pool of money so you can keep betting for long enough to overcome natural variation.  For instance, say we had started with only $2000 when we were playing our 20 games of blackjack.  We can plot a graph of how much money we had over the night:

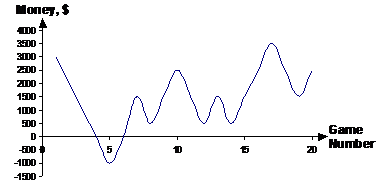
The graph starts showing how much money we have after the 1^st game, which is the initial amount we started with plus the winnings from game 1, making $3000 in total.  Notice how around game 4 the graph dips below the horizontal axis into the negative money region.  This represents actually running out of money.  For instance, after the 5^th game, how am I going to bet money on any more games, when I don’t have any money left?  The simple answer is – I can’t!  This shows the importance of having a large pool of money that won’t run out after runs of ‘bad luck’.  For instance, if we’d started with $10,000, we’d be fine: