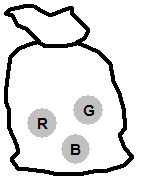
There are lots of events which are not independent.  For instance, say you’re picking marbles out of a bag, and not replacing them.  We can use the example from before where we had a bag with one red, one green and one blue marble in it.  Say we pick a marble out twice – so two events.  The first time we pick a marble out, we’ve got just as much chance of picking any of the three colours.  But the second time we pick a marble out, the probability of picking each of the colours is affected by what marble we took out the first time.  So let’s do a trial run, starting with a sack of three marbles:

We’ve got a 33% chance of picking each of the marbles on our first pick; let’s say that we picked out the green marble on our first pick.  Then we’d be left with this sack:

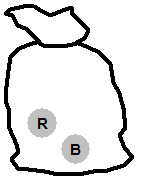
On our second pick, what are our chances of picking each colour marble?  Well, there’s only two marbles left in the bag – red and blue, each one with a 50% probability of being picked.  What’s our chance of picking a green marble out now?  None!  There is 0% probability we’ll pick a green marble out now, since there aren’t any left in the bag.

Now say on our first pick instead of green we’d picked out a red marble.  Then we’d be left with this sack:

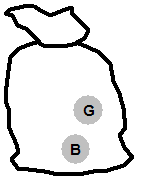
Now on our second pick we have a 50% probability each of picking green or blue, but 0% chance of picking out red.  Compare this case to the last case – now we have a 50% probability of picking green on our second pick, last time it was 0%.  The second event relies or depends on the first event – the second pick is dependent on the first pick.

The test for whether events are dependent is simply the opposite for testing if they are independent.  Two events A and B are dependent if:

                                            

So to work out whether two events are dependent or not, work out the left hand side of this expression using common sense.  Then work out the right hand side of the expression.  If the two sides are equal, then the events are independent.  If they’re not equal, then the two events are dependent.

Say we go back to our marbles in the bag example.  This time, instead of picking out marbles one at a time, we’re going to take two marbles out of the bag at once.  What is the probability of picking out a red and a green marble?  In mathematical notation, what is:

                                                         

Now, using common sense, what is the probability of picking out a red and a green marble at once?  Well, picking two marbles at once, there are only three possible outcomes:

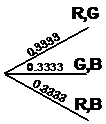
Each outcome is equally likely.  The probability of picking the red and green marbles is 0.3333, or about 33%.  So we know that:

                                                 

Now, if these were independent events, we could also work out this probability by multiplying the two individual probabilities together:

                                                      

The probability of one of the two marbles being red is 0.6666.  The probability of one of the two marbles being green is also 0.6666:

                                        

This is different to the actual probability, so we have shown that these events are dependent, since you can’t work out the probability by multiplying the individual probabilities.  This is shown by the following inequation, showing that the actual probability does not equal the probabilities of each event multiplied by each other.

                                            

If you think about it, the reason you can’t multiply  and  to get  is that each event affects the other. If one of the marbles out of the two you pick out is red, this affects the chance of the second marble being green – the chance of the second marble being green changes to 50%.  changes from being the probability of one of two marbles picked out of three being green (66%), to the probability of one marble picked out of two (the two being a blue and green marble) being green (50%).