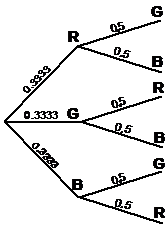More probability

Easy tree diagrams are ones like this one for tossing a coin twice:

To read the tree diagram, you start at the left.  Then, as you read to the right, you get a choice of going along two different paths.  These two paths represent the first coin toss.  The upper path represents getting a ‘head’, the bottom path represents getting a ‘tail’.  If you keep reading more to the right, you get to another two forks – representing the second coin toss.

Joining trees with different outcome spaces

What about for representing a coin tossed once, then a die thrown once.  A coin has only two possible outcomes – heads or tails.  A normal die has six possible outcomes – 1, 2, 3, 4, 5 and 6.  Since the coin is thrown first, the tree diagram starts like the last one:

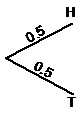
However, now we want to represent the throw of the die.  If we were just throwing a die by itself, its tree diagram would look like this:

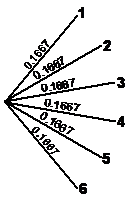
There are six possible outcomes, each with an equal chance (0.1667) of happening.  This whole section is what we need to put on the end of each of the two coin toss outcomes:

To avoid getting it too cluttered up, you often have to resize diagrams so that everything fits nicely in the space – notice how far apart the ‘H’ and ‘T’ forks are from each other.  This is necessary so that the die trees don’t overlap.

Outcome spaces that change through trials

Picking coloured marbles out of a bag is a common probability question.  There are two major types of questions – one where the marble is replaced back in the bag after it is picked out, and one where it’s not replaced.  Say I had a bag with a red, blue and green marble in it.  If I picked a marble out of it twice, replacing the marble back in the bag each time, the tree diagram would look like this:

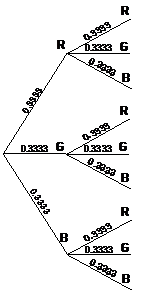
This is the easier of the problems, because each little fork of three paths is the same as the other.  It gets harder when the marbles are not replaced back into the bag however.  The first fork looks the same, but after that, each fork is unique.  For instance, if you follow the top path from left to right, the first time you pick out a marble it is red.  Because you don’t replace it back into the bag, the next time you pull out a marble, there’s only two left in the bag to choose from – the green and blue ones:

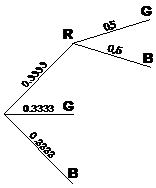
Because after picking the red marble out there’s only two marbles left, the chance of picking the green or blue marbles on the second pick increases to 50% each.  You can do the same thing for the other two first pick choices – green and blue: