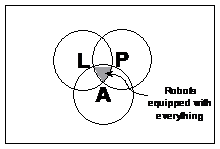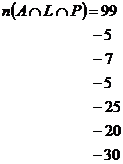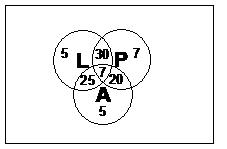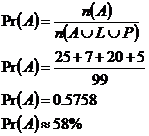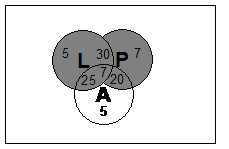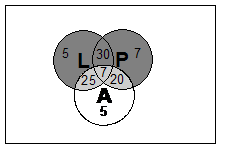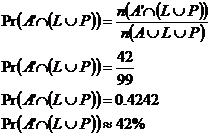Union and Intersection Symbols with Multiple Sets

 means the number of elements in the intersection of set ‘S’ and set ‘R’.  In other words, the number of elements which are part of both sets ‘S’ and ‘R’.  But we can also have expressions which have more than just two sets.  For instance, take a look at this one:

Sponsored Links

                                                         

In the last question, ‘S’ meant swimming, and ‘R’ meant running.  ‘B’ means basketball.  So this expression is asking for the intersection of all three sets – set ‘S’, set ‘R’ and set ‘B’.  In plain English it’s asking us for the students who do swimming and running and basketball.

What about something like this:

                                                         

Notice how now we have union symbols instead of intersection symbols.  This expression is asking us for all the students who belong to one or more of the three sets – ‘S’, ‘R’ and ‘B’.  In plain English, it’s asking us for any student who swims, runs or plays basketball, including students who do more than one activity.

We can get a mixture of union and intersection symbols as well, like this:

                                                       

Now, brackets work like they do in any operation – we work out the things in the brackets first.  So we work on the ‘’ bit first.  This is a union symbol – so it’s saying all the students who are in either set ‘S’ or set ‘R’.  In plain English – all the students who do swimming or running.

Next part is the  bit.  This is an intersection symbol.  So if we put it together with the first bit, we’ve got:

                                                       

                                                                 =

                       (All the students who swim or run) and who play basketball

Notice how I’ve used the brackets in the final expression to emphasise how the sentence should be read.  The instructions that this mathematical expression is telling us are:

·         Find all the students who swim or run

·         From the group found in step 1, pick out the ones who also play basketball

·         The students picked in step 2 are your final set of students

Combining in the other symbols

The ‘not’ symbol can also be used in these mathematical expressions of probability, like this for instance:

                                                           

The expression inside the brackets is an intersection one – asking us for students who do both swimming and running.  But the ‘not’ symbol outside the brackets tells us to take all the students not in the set we’ve just found.  We’ve just found students who do both swimming and running.  So the students not in this set are any students who do not do both swimming and running, or do just basketball.  Using a step by step approach, it would look like:

·         Find the students who do both swimming and running

·         Find all the students who don’t belong to the set found in part 1

·         The students you found in step 2 are your final set of students

You might also get the ‘n’ and the ‘Pr’ symbols.  For instance:

                                                          

The ‘n’ symbol makes this expression mean ‘the number of elements (students in this case) in the set .  This is the number of students who don’t do both swimming and running.

                                                         

The ‘Pr’ in front of the  means the probability of picking a student from the class belonging to the set .  So, the probability of picking a student from the class who does not do both swimming and running.

Combined Venn diagram symbol question

John is just starting his first game of MegaRobotWars.  He gets to jump into his own mechanoid robot machine and try and destroy 99 other robot warriors to win the game.  He’s trying to choose what weapons and armour to mount on his robot, but this will depend on what the other robot warriors he’s facing have as equipment.

5 robots have only turbo lasers, 7 have only plasma rifles and 5 have only reflec armour.  30 robots have turbo lasers and plasma rifles, but no reflec armour.  25 robots have turbo lasers and reflec armour.  Another 20 robots have plasma rifles and reflec armour.  The remaining ‘super’ robots have turbo lasers, plasma rifles and reflec armour.

a) Draw a Venn diagram.  Use ‘L’ for turbo lasers, ‘P’ for plasma rifles, and ‘A’ for armour.

For the first robot John encounters calculate:

                                                           b)

                                                    c)

d) Explain what the probability in part c) represents and how it might be significant

Solution

In this question we have three basic sets – robots which have turbo lasers, robots which have plasma rifles and robots that have armour.  Now, most of the robots don’t have just one of these – most have at least two out of the three possible equipment options.  This means that those robots will be members or elements of multiple sets.  For instance, the 30 robots that have turbo lasers and plasma rifles – they are part of both the turbo laser and the plasma rifle set.

So to draw the Venn diagram, let’s start with three separate circles representing the three basic sets, and work out how they should go together later on:

Stage 1

Now, as the diagram stands in stage 1, we have three different groups of robots, one group armed only with turbo lasers, one group armed only with plasma rifles and one with only armour.  This doesn’t represent what we are trying to – lots of the robots have more than one type of equipment.  The ‘super’ robots have all three pieces of equipment fitted.  We can represent these by drawing the three circles so that they all overlap somewhat:

Stage 2

The shaded area in the middle of the diagram represents the intersection point of all three sets – so robots inside this shaded area are armed with turbo lasers and pulse rifles and have reflec armour.  Notice how there are also areas in the diagram where only two sets overlap:

Now, we have actual numbers of how many robots there are equipped in each way, so we can label the diagram with numbers.  For instance, only 5 robots have just turbo lasers, so we put a ‘5’ in the top left circle.  The ‘super’ robots are represented by the central area – to work out how many of those there are we need to subtract all the other robot numbers from the total of 99.

We can actually write this all in a mathematical form, using our set notation.  In English, what we’re doing is:

Each term in this expression can be written using proper set and probability notation.  For instance, the super robots are the robots that have everything.  In other words, they are the robots at the intersection of all three sets.  So the number of super robots can be written:

                                                      

The total number of robots is just the union of all three sets:

                                                      

The number of robots that have only lasers is a bit trickier to write.  It’s not .  That means all the robots that have lasers, including ones with other equipment.  We want those with only lasers.  So we want the robots that don’t have armour or plasma rifles, but do have lasers:

                                                     

Keep on doing this for the other groups and you should eventually get, as a mathematical replacement for the long word expression earlier:

                     

Now, there is enough information in the question to substitute in for each of these terms:

                                                  

                                                   

So there are 7 ‘super’ robots.  This was a long winded way of going about it, but it contained lots of practice at converting everyday English expressions into mathematical notation.  With this last piece of information, we can label every bit of the Venn diagram with a number of robots:

A good check at this stage is to see whether all the separate areas of the Venn diagram add up to the total number of robots.  In this case, 5 + 30 + 7 + 7 + 25 + 20 + 5 does add up to 99, so it’s OK.

b)

 is pretty easy to find – what we need to do is find how many robots have armour, and divide that by the total number of robots to get the probability.  The number of robots that have armour is calculated by adding up all the numbers within the ‘armour’ circle on the Venn diagram:

                                               

c)

 – what does this mean?  Well, let’s interpret the inner brackets bit first -  is the union of ‘L’ and ‘P’ – so all robots which have either a laser or plasma rifle or both:

However, there’s this other  bit.  This  part is all robots that don’t have armour.  When combined with the intersection symbol, it means of the  robots, all the ones that don’t have armour.  So this means we have to get rid of all the shaded areas which are in the ‘A’ circle:

Now all we have to do is add up the numbers inside this shaded area:

                                                     

So 42 robots fit into the set described by .  To find the probability, we divide this number of robots by the total number of robots:

                                       

d) This is one of those horrible non-specific questions.  The first part we can answer at least – the answer to part c) represents the probability of the first robot John encounters having lasers and/or plasma rifles, but no armour.  But what about the significance of this? 

Well, these questions can be answered by thinking about the context of the question – what it’s about.  In this case, John is obviously trying to destroy all the other robots to win the game.  What might be significant about encountering a robot with weapons but no armour?  Well, because the robot may not have any armour, John might be able to destroy it quickly with his robot.  So this 42% probability is significant in that it represents the chance that the first robot John encounters will be easy to quickly destroy because it has no armour.