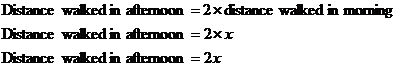Algebraic translation question

John walked a certain distance in the morning, before he had lunch.  Then in the afternoon, John walked twice as far as he had in the morning.  In total that day John walked 27 km.  How far did John walk in the morning?

Solution

First things first.  We can say with a fair amount of confidence that the solution to this problem will involve algebra, as the question is in the algebra section of this book.  The general trick with these questions is to try and assign algebraic variables to quantities or amounts in the question.  This will often get you started.

So in this question what quantities or amounts are there.  Well there’s John, but he’s not really a quantity – he’s just a person.  What about lunch – well that’s just a meal, not really an amount or a quantity.  What about the distance John walked – bingo!  The distance he walked is a quantity – it’s some number of kilometres.

Now, in general, you need to assign variables to represent quantities that you don’t know anything about.  So, let’s think about distances.  John walked a certain distance in the morning.  He also walked another distance in the afternoon.  And then there’s the total distance he walked during the whole day.  However, we know this last amount – he walked 27 km during the whole day.  So the unknown amounts are how far he walked in the morning and how far he walked in the afternoon.

So, what we can do is assign an algebraic variable to represent one of these unknown quantities – let’s start with the distance that John walked in the morning, since this is the amount we’re trying to find out:

                            Let x = the distance that John walked in the morning

So now we’ve written a simple sentence telling the reader that ‘x’ now represents the distance that John walked in the morning.

Another thing that will help you get started in many algebraic problems is to look for relationships between quantities in the question.  In this question for instance, there is a relationship between the distance John walked in the morning and the distance he walked in the afternoon.  He walked twice as far in the afternoon as he did in the morning.  We can add this to our solution:

This should make sense – in the afternoon he walked twice as far, so he walked a distance of ‘2x’ in the afternoon, compared with only ‘x’ in the morning.

So, we still need to find out how many kilometres John walked in the morning – in other words we have to find out what ‘x’ equals.  We need to write an algebraic equation relating ‘x’ to some number.  The only number in this question we have been given is the total number of kilometres John walked in the day – 27 km. 

We already have algebraic expressions for the distance John walked in the morning and afternoon – we can join these together to give the total distance he walked in the day:

Now all we have to remember is to write the answer at the end of our solution:

                                   Answer: John walked 9 km in the morning.