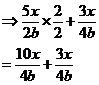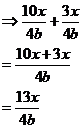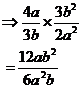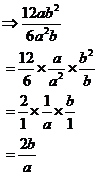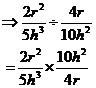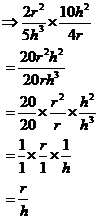Fractions don’t have to have only numbers in them. They can also have algebraic variables in them as well. And you also need to be able to add, subtract, multiply and divide algebraic fractions together just like you do with normal number only fractions. However, the rules are the same as for working with number fractions.
Adding algebraic fractions
|
Algebraic fraction addition problem Sponsored Links |
|
Calculate |
|
Solution |
|
First thing we have to is get the two fractions to have a common denominator (i.e. have the same thing on the bottom as each other). We can do this by multiplying the tops and bottoms of the left fraction by 2: Now we’ve got a common denominator, we can do the rest of the calculation: Subtraction is just like addition – you need to make sure all the fractions have a common denominator. Now for multiplication and division. |
Multiplying algebraic fractions
|
Calculate |
|
Solution |
|
Multiplication just means we have to multiply the tops by the tops (the numerators), and the bottoms by the bottoms (the denominators): We also need to simplify it by cancelling out bits. · 12 divided 6 becomes 2 on the top · ‘a’ divided by ‘a2’ becomes just ‘a’ on the bottom. · ‘b2’ divided by ‘b’ becomes just ‘b’ on the top. |
Dividing algebraic fractions
|
Calculate |
|
Solution |
|
The trick to dividing is to change it to a multiplication,
by swapping the top and bottom of the fraction that is doing the dividing.
In this case, the Now we can just calculate an answer like a normal multiplication: |
.
is the fraction that is being
divided, and 
is the fraction that is doing
the dividing. So we can turn this into a multiplication by swapping the
tops and bottoms of the 
Handy Hint #1 - Confusing ‘x’ and ‘×’
This is one of the most common mistakes made in exams – when students don’t notice the difference between a multiplication operation (×) and an ‘x’ symbol. When you’re doing algebraic problems you want to make sure that these two things look really, really different. And remember, even though you may be able to tell the difference, what about your teacher, who may be marking your exam late at night in bad lighting conditions when their eyes are tired. It’s best to play safe. For instance, I draw my ‘x’s as if they were made up of two ‘c’s put together, with one of the ‘c’s back to front. My multiplication symbols are smaller and made up of two straight lines, like this:
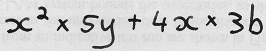
You can use whatever style you want, as long as it is clear to anyone reading it what the difference is between the two symbols.
