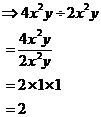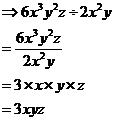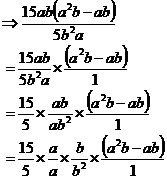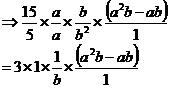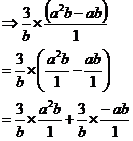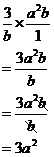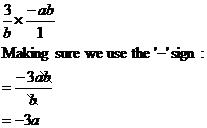Multiplication And Division In Algebra

Clear explanations and worked examples from the Math-Mate school maths textbook.

Multiplying and dividing algebraic variables can be confusing when you first start algebra. One of the things you must always remember is that when you have something like:

this is really

It’s just that we often don’t write the multiplication symbol in when we’re writing algebraic expressions.

Another thing it is important to remember is that:

When you have a variable raised to the power of 2 or 3, it is simply a shorter way of writing all the multiplication symbols in.

So say we have a question like:

Unlike addition and subtraction, to perform multiplication and division you do not need like terms. Instead, you are looking to combine variables together. So, first of all, I can rewrite this expression, but separating out all the different bits:

I can further rewrite this expression by putting all the similar variables together:

Now I have all the numbers at the front, the ‘x’ parts in the middle and the ‘y’ parts at the end. I can start to simplify the expression by combining similar parts. Firstly, I can see a ‘2’ and a ‘4’ multiplied by each other – I know that so the expression becomes:

Next, I can deal with the part – remember that , so this is really just , which is the same as . So the overall expression becomes:

The last bit I have to deal with is the bit. Another way of writing this would be . When you multiply two of the same variables together, you can just add their powers (the little numbers above the right hand side of the number). So . So now the overall expression becomes:

The last step is to remove the multiplication symbols, since they are not usually written in this type of algebraic expression:

and voila! There’s your answer.

Now, how about some expressions that involve division as well:

I have often found it easier to rewrite this using a fraction instead of a ‘÷’ sign, like this:

This way you can easily separate the expression into parts containing the same variables:

Now, the first part of this expression is easy to simplify – it’s just 8 divided by 4, which we all know is 2. Our overall expression becomes:

Next we have to look at the divided by part. The easiest way to do this is to remember that , so it’s really:

When you divide two of the same variables, you can just subtract the 2^nd power from the first one:

So the overall expression becomes:

The last bit to do is simply the part with the ‘k’s in it. This is easy to do:

So the overall expression becomes:

Remove the multiplication symbols, because they’re not usually written, and we get:

Brackets in algebra

Brackets are used in algebra to show that some type of operation needs to be done on a number of terms, rather than just one. For instance, if I want to multiply 3x by 4, I just go:

But what if I need to multiply by 2? I could go:

but this is a bit awkward and looks messy. A much neater way to write it is to use brackets:

This expression tells me that everything in the brackets needs to be multiplied by 2.

Factors in algebra

Numbers can have factors. Factors can be multiplied together to give the number. For instance, the factors of 10 are 1, 10, 2, and 5. This is because you can get 10 from them by doing:

But you can also have factors in algebra. Take the following expression for instance:

If I read this out aloud, it would sound something like, “four times x squared times y.” I can also split this expression up into smaller bits like this:

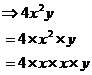
By splitting it up, what I have done is work out what all its factors are. When we’re using numbers, factors multiply together to give the final number. When we’re using algebraic variables, factors multiply together to give the final algebraic expression. So the factors of are .

Highest common factor in algebra

When you have two algebraic expressions, the highest factor of both expressions is called the highest common factor, or greatest common factor. Say I had the following expressions:

and

To find the highest common factors I like to go through each expression bit by bit. So first, I compare the two number parts – the ‘4’ and the ‘6’. The highest common factor of 4 and 6 is 2, so I write down 2:

HCF (Highest Common Factor) = 2…

The ‘…’ after the 2 means I haven’t finished writing down what the HCF is. Next, I move on to the next bit – the ‘x’ part. In the first expression, we have a ‘’, in the second expression we have a ‘’. The highest common factors of these two bits is ‘’. So I write that down after the ‘2’:

HCF (Highest Common Factor) = 2x²…

Now we can move on to the next bit of the two expressions – the ‘y’ bit. The first expression has a ‘y’, the second expression has a ‘y²’. This means the HCF of this part is simply ‘y’. I can write that down in my answer:

HCF (Highest Common Factor) = 2x²y…

The last bit of the expressions I look at is the ‘z’ bit. However, z is only in the second expression, not the first. This means there is no common factor between the two expressions for ‘z’. So I can’t write down anything more. This means my answer is:

HCF = 2x²y

If you’ve got time, it pays to check whether this answer makes sense. You can do this by trying to divide both expressions by the HCF, and seeing if you can get an answer. Let’s do that now:

Two things to look for here. First of all, you should be able to do the division without getting any fractions or decimals in your answer. That checks out in this case. The second thing is to look to see if there are any more common factors between your two answers. If there are, you need to multiply your original answer by that common factor. In this case, there are no common factors for ‘2’ and ‘3xyz’, so it looks like our answer is correct.

Factorising algebra - using common factors to introduce brackets

Brackets can be used to make algebraic expressions much more neat looking and easier to work with. Take the following expression for instance:

Looking at this expression, you can see straightaway that there are a lot of common factors – there are ‘q’s and ‘j’s in both expressions for instance. You can factorise this expression by finding the highest common factor and putting the expression into factorised form. Watch this:

Handy Hint #1 - Introducing brackets in algebra

Find the highest common factor:

For the numbers part, the HCF is 5.

For the ‘q’s, the HCF is q².

For the ‘j’ part the HCF is j.

So the overall HCF is 5q²j.

Take this HCF and put it outside a pair of brackets with some space between them:

Now we need to write something inside the brackets. The thing to write is the original expression, divided by the HCF like this:

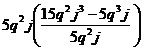
Now look at this expression. If we multiplied the bottom of the fraction by the factor outside the brackets, we’d end up with our original expression. But since we’re factorising, let’s just simplify what’s inside the brackets:

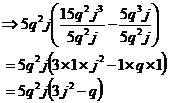
If you’ve got heaps of spare time, you can multiply out the brackets to check you get back to your original expression in expanded form. It is useful to be able to switch between expanded form and factorised form quickly and easily.

Mathematical diagram

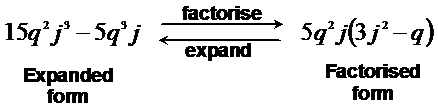
So let’s try a reasonably complex algebraic simplification problem:

Complex algebraic simplification problem

Simplify

Solution

So this expression has brackets, multiplication, division, subtraction and addition in it. Brackets are the first operation we need to do, so we look at them first:

Can we simplify what is in the brackets? Well, there are two terms, the 2^nd term () is being subtracted from the first term (). Now we can only do the subtraction if they are like terms. Like terms have to have the same variables raised to the same powers. Both these terms have the variables ‘a’ and ‘b’, so that’s ok. But a is raised to different powers in each term, so they are not like terms. This means we can’t simplify what’s within the brackets.

So now we can look at the whole expression and spread it out:

In each step I’ve just done a little bit of re-arranging, trying to separate the expression into bits which only have one variable in them. Now I can simplify each bit at a time:

The becomes 3 and the becomes 1. The is the same as , which if you remember is:

Any variable or number raised to a negative power is the same as 1 on that variable raised to the positive of that power:

So the whole expression becomes:

Now we have to multiply out the brackets. Firstly, we know that we have to multiply each term in the brackets by . So we can rewrite the expression to show this:

Now there are two multiplication operations we have to do. To multiply fractions we multiply the tops together and the bottoms together. The first one is:

Mathematical diagram

The second multiplication is:

Mathematical diagram

So overall we have:

This can be made a little bit more elegant by using more brackets, although it’s more a matter of taste: