Some of the first questions you get when you start algebra are to simplify expressions. For instance, say you had to simplify the following expression:
![]()
Sponsored Links
So, when you look at this expression, one thing you can do straight away is work out that there are 6 terms. To simplify the equation, you need to search for like terms:
![]()
In this expression there are 3 sets of like terms. The first set contains terms with an ‘x2’ in them – these have a circle around them. The second set of like terms have only ‘x’ in them – these have a rectangle around them. The last set of like terms are just the numeric terms – these have a diamond shape around them.
Since the only operations in this expression are additions and subtractions, we can re-order the terms. By re-ordering the terms, we can have like terms next to each other, which makes the expression a lot easier to simplify:
So ![]()
becomes
![]()
and now we have each set of like terms together – the ‘x2’ terms are at the start, the ‘x’ terms are in the middle, and the numeric terms are at the end. Now to simplify the expression, we just need to add or subtract the like terms:
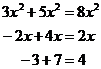
So the overall expression becomes:
![]()
Notice how there are no like terms in this expression anymore – each term is different. This is a good way to check you have done as much simplification as possible. If there are still like terms in the expression you haven’t finished simplifying.

