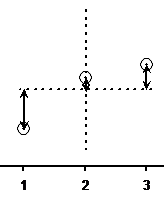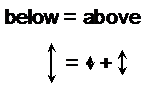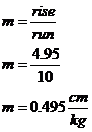The quickest way to draw a line of best fit is to draw one following these simple steps:
Sponsored Links
· Draw a vertical line that splits the points up into two equal sized groups. If there are an odd number of points (for instance 5), just split the groups slightly unevenly (3 in one, 2 in the other).
· Find the middle of each group in the horizontal direction.
· Find the middle of each group in the vertical direction.
· Draw a cross or marker at the midpoint of each of the two groups. The midpoint is the location found in steps 2 and 3.
· Draw a line between these two midpoints.
So, using our graph as an example, here are the steps:
Step 1.

Step 2.

In the left group, the middle of the group horizontally has been marked with a dotted line. It passes exactly through the middle point in this group because we want the amount of space between it and points on the left of the dotted line to equal the amount of space between it and points on the right of it. Same goes for the right group of points.
Step 3.

Look at the left group of points. Notice how the dotted line representing the middle of the group vertically does not pass through the middle point in the group. This is because we want the amount of space between the line and points above it to be the same as between it and points below it:
|
Left Group |
|
|
|
|
Step 4.

Step 5.

Easy! Because you’re estimating things by eye, this method does not give you a perfect line of best fit, but it’s pretty good, and is quick to do.
This line of best fit is a straight line. Sometimes you’re better off using a curved line to represent the data. For instance, say we got given this data:

The points seem to trace out more of a curve than a straight line – so to draw a line of best fit we could be better off using a curved line. You can try both and see which one gives you a better fit:

Notice how the curved line seems to fit the data points a lot better than the straight line.
|
James and Jenny are trying to find a formula that will tell them how far a spring will stretch when they hang weights off it. Based on the data they collected, find a formula that gives the amount of stretch, given a certain weight.
|
||||||||||||||
|
Solution |
||||||||||||||
|
Well, we’ve got a table with two variables in it – weight and stretch length. From glancing at the data, it seems that the more weight is put on the spring, the further it stretches (which makes sense). What we want to find out is what exactly this relationship is so we can answer the question, “how far would ‘x’ kilograms make the spring stretch?” We can see what type of relationship there is by plotting the data on a graph. Now, one of the variables is going to be on the horizontal axis and the other on the vertical axis. Usually, the independent variable is plotted on the horizontal axis. This is the thing which we set or determine in the experiment – in this case James and Jenny have set various weights to put on the spring, so we’ll put weight on the horizontal axis. The dependent variable is usually plotted on the vertical axis. This is the thing which depends on the other variable(s) – in this experiment the stretch length depends on how much weight is put on the spring – so we’ll plot stretch on the vertical axis:
This graph immediately tells us about the relationship – it looks like you could fit a straight line through the data pretty easily. This tells us there is a linear relationship between the weight on the spring and how far it stretches. So if we go ahead and use the visual method of drawing a line of best fit: First splitting it up into two equal groups of points:
Then finding the midpoints of each group in the horizontal and vertical directions:
Then drawing a cross where the midpoint of each group is and connecting the midpoints by a straight line:
We are looking for a formula that tells us how much the spring will stretch if we put a certain amount of weight on it. We can get this by finding the equation of the best fit line. Normally, this equation is written with variables ‘x’ and ‘y’: But instead of ‘x’ we have the weight, ‘w’. Instead of ‘y’ we have the stretch length, we’ll call ‘s’: If we can find out the value of ‘m’ and ‘c’ we’ll have a formula. Now, ‘m’ is the slope of the line, and ‘c’ is the intercept on the vertical axis, which is the stretch axis in this question:
The intercept, ‘c’, is going to equal ‘0’. To work out the slope I’ve taken two points at each end of the line – one point at the origin, and one point at (10 kg, 4.95 cm). Using these two points I’ve worked out the rise and the run. The slope ‘m’ is equal to the rise divided by the run: So if we put these values of ‘c’ and ‘m’ we’ve found back into our line equation, we get: And that’s our formula for the stretch in this spring based on the weight put on it. It tells us that for every kilogram of weight put on the spring, the spring will stretch about half a centimetre. |