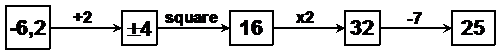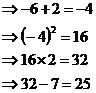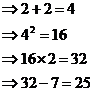Equations using box stories
Box stories are a visual way of showing how to form an equation. If you understand equations well, then they don’t really help you much in a practical sense, but they do make it easy to see how each part of the equation comes about. The basic theory behind box stories is that you have boxes in a line filled with numbers or variables, with lines connecting the boxes showing what operations should be performed. For instance, take this simple expression:
Sponsored Links
If I were to write how to get this expression in words, I’d have something like this:
“Take x, multiply it by two, and then add three”
Now, to form a box story, you always need to start with a box. In this case, the first thing we start with is just ‘x’, so let’s put that in our first box:
The very next thing that happens is that this ‘x’ is multiplied by ‘2’. This is an operation – a multiplication operation. So we use a horizontal arrow and write the operation just above it:
Now, whenever we perform an operation, there is always a result of that operation. This result can be shown in another box attached to the end of the operation arrow. In this case, we’ve multiplied ‘x’ by ‘2’, so our result is ‘2x’:
What’s the next operation that we need to perform? Well, we need to add ‘3’ to our current result:
Last thing we need to do is write the result of this last operation in a new box:
This sequence of boxes and lines tells the story of how this equation was formed. Notice how it neatly alternates between boxes and lines as you read from left to right. So you always start with a number or variable, then perform an operation on it, get another result, perform another operation on this result, get a new result…etc.
The boxes don’t all have to be the same size. As you get towards the end of an equation, the result in each box is going to usually get longer, so you might have to use a larger box.
Working backwards
Often you get given a final result, and also the sequence of operations that were used to get that final result, and are asked to find the initial number. For this type of question, you need to represent the initial number with some variable, say ‘x’, and write out the box story, but without filling in the boxes, except for the first and last one. For instance:
|
If I take a number, add two to it, square it, multiply it by two, and subtract seven I end up with 25. What’s the number? |
|
Solution |
|
All we need to do is write out the box story. Let’s call this unknown starting number ‘x’. We can write out the box story, but remembering not to fill in any of the boxes except the first one (which has ‘x’ in it) and the last one (which has the final result, ‘25’, in it):
To find out what the value of ‘x’ is, we need to work backwards through the box story. When you go backwards (from right to left), you do the opposite of what each operation tells you. So for instance, when we go from the ‘25’ box through the ‘–7’ operation, we need to add 7 instead of subtracting 7:
This gives us ‘32’ in the result box. The next operation tells us to multiply by 2, but since we’re going in the opposite direction, we do the opposite – we divide by 2:
If we look at the next operation, it tells us that
whatever’s in the blank box, when squared, it equals 16. We’re in the
situation of
The last operation says to add two, so we need to subtract two. The two numbers we’re subtracting two from are positive four and negative four, so we get:
In the final step we just did, we replace the ‘x’ with the values that it can be – negative six or positive two. To check our answers you can work forwards through the box story to check you end up with 25 for both values of ‘x’:
|
, and we’re trying to find the
value of ‘something’ by taking the square root of 16. This means we need to
take into account both positive and negative possibilities:
:
:
