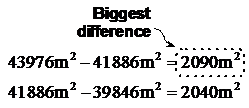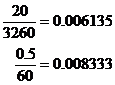Calculations With Numbers That Have Errors

Say I’m measuring a room which is about 5 metres long, but I’ve only got a 4 metre tape measure. I’ve also got a 1 metre ruler as well, so what I do is extend the tape measure to measure 4 metres, and then I measure the last metre with the ruler. The measurements I get, with their errors, are:

Adding and subtracting numbers with errors

When you add or subtract two numbers with errors, you just add the errors (you add the errors regardless of whether the numbers are being added or subtracted).

So for our room measurement case, we need to add the ‘0.01 m’ and ‘0.005 m’ errors together, to get ‘0.015 m’ as our final error. We just need to put this on the end of our added measurements:

You can show how this works by considering the two extreme cases that could happen. Say the measurement with our tape measure was over by the maximum amount – when we measured 4 m it was actually 3.99 m. Let’s also say that the ruler measurement was over as well by the maximum amount – so when we measured 1.00 m it was really 0.995 m. If we add these two amounts together, we get:

This number is exactly the same as the lower limit of our error estimate for our added measurements:

You’d find it would also work if you considered the opposite case – if our measurements were less than the actual distances.

Adding or subtracting an exact number

The error doesn’t change when you do something like this:

Multiplication or division by an exact number

If you have an exact number multiplying or dividing a number with an error in it, you just multiply/divide both the number and the error by the exact number. For instance:

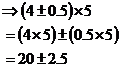
Multiplication of numbers with errors

Say we had these two numbers and were multiplying them together:

The big mistake a lot of people do time and time again is just to multiply together the two numbers and also multiply the two errors together to get this:

This is wrong wrong wrong! This implies that the smallest the answer could be is 27.995 and the largest it could be is 28.005. Let’s see what we get when we multiply the two numbers together assuming that the numbers were actually 4.05 and 7.01:

This is much bigger than 28.005, showing that multiplying the two errors together doesn’t work! If we take the other extreme and assume the numbers were actually 3.95 and 6.9, we get:

This number is a lot smaller than 27.995, showing once again that multiplying the two errors doesn’t work.

Errors in multiplication – simple absolute error method

Let’s take two general numbers ‘a’ and ‘b’, with errors ‘x’ & ‘y’, and multiply them together:

Now, usually the errors are much smaller numbers than the numbers themselves. When this is true, the ‘xy’ term can be ignored, since it’s a small number multiplied by another small number, which gives you a very, very small number, compared to the ‘ay’ and ‘xb’ terms. This leaves us with:

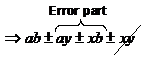
The error is going to be biggest when either both ‘ay’ and ‘xb’ are positive, or when both are negative. So, the error when you multiply two quantities together is:

This method is never perfect, but works best when the errors are much smaller than the actual numbers. Here’s the method applied to the multiplication above:

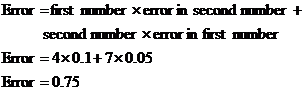
Errors in multiplication – simple relative error method

You can also work out the error in your final answer by working with the relative errors:

The relative error in the result of a multiplication is the sum of the relative errors of the two numbers being multiplied.

For example:

First work out the answer just using the numbers, forgetting about errors:

Work out the relative errors in each number:

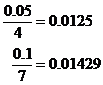
Add them together:

This value is the relative error in the value you get multiplying the two numbers together – 4 by 7 gives 28. We could write this as a percentage error (remember to multiply it by 100 to turn it into a percentage):

To write the answer with an absolute error, we need to multiply the 28 by the relative error:

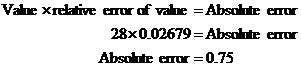
This means our final answer is:

Notice how we get the same answer using either the absolute error method or the relative error method.

Multiplication of two numbers with large errors – long method

When the two numbers you’re multiplying together have errors which are large, the assumption that multiplying the errors by each other gives a very small result isn’t true anymore. When that happens, all you can do is calculate the two worst case scenarios and then work out which has the larger error and use that:

For instance, when we multiplied 4 and 7 together before, we calculated the smallest and largest answers you could get with the error amount specified for each number:

Largest Possible Number

Smallest Possible Number

To find the largest possible number, we just assumed each number had the maximum positive error (+0.05 for the 4 and +0.1 for the 7). To find the smallest possible number, we just assumed that each number had the most negative possible error (–0.05 for the 4 and –0.1 for the 7).

Now we want an answer in this form:

To work out the error, you just need to find the largest difference between the answer you get (28) by multiplying the two numbers only together and the two extreme cases. So we have to work out which is further from 28 – 28.755 or 27.255:

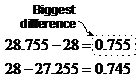
This means we need to use ‘0.755’ as our error in the final answer. So the completed final answer would be:

Because the errors for each number are only given to one significant figure, we really should round our error up to one significant figure as well:

There isn’t any real way to shortcut this process when the errors are ‘large’ relative to the actual numbers. Because there are three terms that affect the error (since the product of the two errors can’t be ignored when the errors are large), you can’t really predict whether the error will be largest when each number’s error is positive or negative. That’s why you need to work out the answer you’d get for both cases, and then work out which one gives the biggest error.

Assuming small errors – simple methods

No assumptions – long method

We can compare the answer we got this way with the answer we got using the simple methods. ‘0.75’ is pretty close to ‘0.755’, it’s not perfect, but it shows the simple method works pretty well as long as the errors aren’t too large compared to the numbers themselves.

Division with two numbers with small errors – simple relative error method

When the errors are small compared to the numbers themselves, you can work out the error in your answer by working with the relative errors (the error divided by the number itself).

The relative error in the result of a division is the relative error in the numerator plus the relative error in the denominator.

Here’s an example calculation:

First work out the answer you get just using the numbers, forgetting about errors:

Then work out the relative errors in each number:

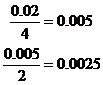
Add the relative errors together:

This is the relative error in the result of dividing 4 by 2, which is 2. If we want to convert this back into an absolute error, we need to multiply our answer 2 by 0.0075:

So the final answer is:

Division with two numbers with large errors – long method

Same thing applies here as for multiplication – you need to work out the two extreme cases. However, how you go about doing this is different to for multiplication. For multiplication, when we were trying to find out the largest possible answer we assumed that both errors were as positive as possible. To get the largest number possible in the case of division however, what you want to do is use the largest positive error for the number being divided, and the largest negative error for the number doing the dividing.

To find the smallest possible answer you do the reverse – you use the largest negative error for the number being divided, and the largest positive error for the number doing the dividing. After doing this you work out which extreme is further from the answer you get when you do the division with the numbers only, and use this difference as your final answer. For example:

The answer I get doing the division just using the numbers is:

To find the largest possible answer, I use the positive error for the number being divided, and the negative error for the number doing the dividing:

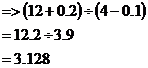
To find the smallest possible answer, I use the negative error for the number being divided, and the positive error for the number doing the dividing:

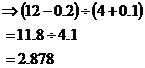
Now I just need to work out which extreme is further from the answer, and use that as the error range:

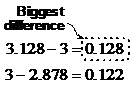
So my final answer will be:

And rounded to one significant figure for the error:

If we used the simple relative error method for this calculation, we would have got this:

Calculate answer using just the numbers, forgetting about errors:

Relative errors in each number:

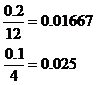
Add these together:

Write the answer using a percentage error:

Convert the relative error into an absolute error:

Write the answer using an absolute error:

Assuming small errors – simple methods

No assumptions – long method

As you can see, the simple method works fairly well for this division as well.

When is an error large enough to use the long method?

For addition and subtraction, finding the final error in the answer is easy. For multiplication and division however, we’ve got two methods. When the errors are ‘small’ enough relative to the numbers involved, the final error can just be calculated using one of the ‘simple’ methods.

But when the errors are ‘large’ relative to the actual numbers, then you need to follow the long procedure, summarised here:

· Work out the number only answer, forgetting about errors, by simply multiplying or dividing the two numbers

· Find the largest and smallest answers you could get given the errors specified for each number in the calculation

· Work out which extreme is further from the number only answer

· Use the difference between this extreme and the number only answer as your final error

I generally use the simple methods (which assume the errors are small compared to the numbers) if the errors are less than 1% the size of the numbers. In other words, I use the simple methods if the percentage error in each number is less than 1%. See what is acceptable for your teachers, they might require you to always be as accurate as possible, in which case you’d never use the simple methods. Or they might prefer the simple methods and tell you to use them all the time.

Land block sizing question

Lengths and areas of blocks of land are a common topic for questions which involve working out errors.

a) Jon’s got a block of land, which from reading 50 year old documents is supposed to be 234 metres by 179 metres. However, the dodgy measuring they did back then was only accurate to within 5 metres. What’s the total area and the error in this value?

b) Jon also has another rectangular block of land which has an area of . He knows the length of one side of the block is . What’s the length of the other side of the block, and the error in this length?

Solution

a) The first part of this question is a multiplication problem:

Since the errors are larger than 1% of the numbers, I’m going to use the long method where we work out the two extreme values our answer could have.

First work out the number only answer:

Now work out the largest and smallest answers I could get:

The largest:

The smallest:

Work out which one is further from the number only answer:

So the total area is:

To an appropriate number of significant figures it’s:

b) This part of the problem is a division problem, since we know the area of a rectangle and the length of one of its sides. To get the other side length, we need to divide the area by the known length:

Since both errors are smaller than 1% of the numbers they’re associated with, I’m going to use the simple relative error technique to work out the final answer:

First, work out the number only answer:

Then, work out the relative errors for each of the two numbers:

Now add these relative errors together:

This is the relative error in our final answer, 54.33 metres. To convert it into an absolute error, we need to multiply it by our final answer:

So the unknown side length of Jon’s second piece of land is:

To an appropriate number of significant figures it’s: