Working with errors and measurement
In everyday life you often hear people using the words ‘accurate’ or ‘precise’. In mathematics and engineering these two words have a very specific meaning, and they are different! The most common way of explaining what they mean is to talk about an archer shooting arrows at a target:
Sponsored Links
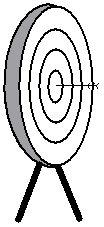
Accuracy is all about how close to what you’re aiming for you get. For instance, in archery, you’re trying to get as close to a bullseye as possible (an arrow hitting the circular target exactly in the centre).
|
A very accurate shot |
A not so accurate shot |
Precision on the other hand is all about how close repeated shots are to each other. Precision has nothing to do however with how close you are to your desired goal. So if the archer shoots a few arrows at the target and they end up grouped closely together, he has been precise, regardless of whether they’re near the bullseye or not:
|
Precision and accuracy |
Precision but bad accuracy |
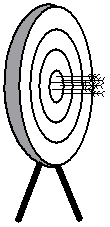
The diagram on the left shows arrows bunched closely together at the bullseye. Because they’re bunched closely together, the archer has been precise. Because they’re all near the bullseye, it also means the archer has been accurate.
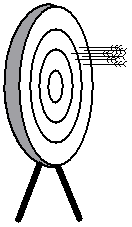
The diagram on the right shows the arrows bunched closely together, but nowhere near the bullseye. Because they’re bunched closely, the archer’s been precise, but because they’re nowhere near the bullseye, the archer’s accuracy hasn’t been very good.
It is possible to be precise, but not accurate – the diagram above on the right shows an example of this. However, it is not possible to be accurate unless you’re precise.
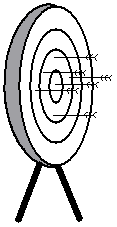
The following diagram shows arrows that are grouped around the bullseye, but not very closely. Because the archer has had very bad precision in this case, most of the arrows are a fair way from the bullseye, so this means he has not been very accurate either.