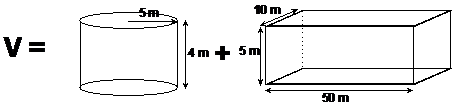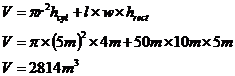Some questions will tell you to assume that the surface of a shape has a certain thickness, and then ask you to find the volume of this ‘thick’ surface. For instance, in the previous question about a pool, you might be told that the pool needs to have 5 cm thick walls and a 5 cm thick bottom.
Sponsored Links
To solve these questions, what you need to do first is find the surface area of the part of the shape that has this thickness. Be careful here, sometimes it won’t be the whole shape – for instance with a pool there is no concrete layer on the top of the pool – that’s where the surface of the water is!
So you might split up a shape into each of its surfaces like this:
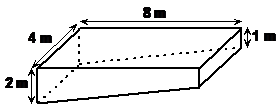
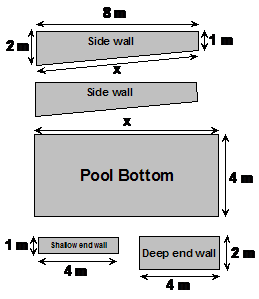
There’s one dimension we need to work out before we can solve the problem – the length of the pool along its sloping bottom. We can use Pythagoras’ Theorem to help us do this:
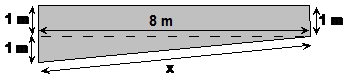
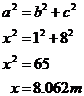
Now we can work out the entire surface area of the walls and pool bottom. We have already worked out in the previous section that the side walls have an area of 12 m2 each:
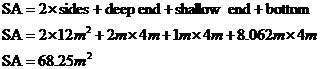
The question says that the thickness of the walls and bottom is 5 cm – this is 0.05 metres. All you need to do is multiply the surface area of the walls and bottom by this thickness:
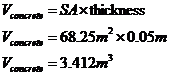
|
Bob’s tanker ship has three internal tanks to hold oil. The main tank is a rectangular prism as shown in the diagram. At each end of the ship there is a tank shaped like a half cylinder, with a diameter of 10 metres and a height of 4 metres. How much oil in kilolitres can Bob’s tanker hold?
|
|
Solution |
|
Well, the tanker’s internal tank volume is made up of three solid shapes – a rectangular prism, and two half cylinders. If we were to put the two half cylinders together, they’d make up a whole cylinder, so we can think of the problem as being:
A kilolitre is 1 cubic metre of fluid, so the final answer is: The largest oil tankers in the world can carry a lot more than this, the Jahre Viking is the largest ship in the world, and can carry around half a million kilolitres of oil! |