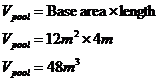Volumes of composite solid shapes
It’s not really that different finding volumes of composite shapes compared with finding surface areas. You’ve just to remember to not mix up formulas between the two!
A lot of questions will give you two dimensional diagrams of a 3 dimensional shape, and tell you the information about the third dimension. For instance, you might get an overhead diagram of a pool (what it would look like as if you were hovering in the air directly over it):
Sponsored Links

The question might say something like “the pool linearly increases in depth from the shallow end to the deep end”. Now, for you to solve the question, you really need to have a 3-dimensional image in your head of what the pool looks like. We know that the top of the pool is a rectangle 8 m by 4 metres, and we can assume that the bottom of the pool is also a rectangle, since there’s no information in the question to suggest otherwise.
Also, we can work out that the shallow end and deep end sides must be rectangles. The shallow end side will be a rectangle 1 metre by 4 metres, the deep end rectangle 2 metres by 4 metres. The hard bits to work out are the sides of the pool that run along the 8 metre length. But if we draw the rest of the diagram first, they’re not so hard to work out. Here’s the rest of the diagram first:

We can add in the sides that run along the length of the pool simply by drawing two more lines in our diagram. Then we can label all the dimensions that we know:
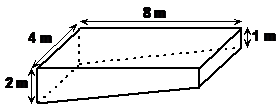
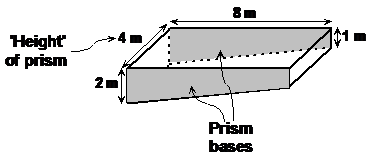
Now, with a 3D diagram, the question becomes easy to solve. Looking at the diagram, we can see that the long sides of the pool form the bases of a prism. To work out the volume of a prism, all you need to do is work out the area of the base, and multiply that by the ‘height’ or ‘length’ of the prism (distance between the two bases).
The base shape is a trapezoid, we can work out its area this way:

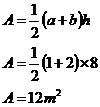
Now all we need to do is multiply this base area by the ‘length’ or ‘height’ of the prism – the distance between the two bases. In this case, this distance corresponds to the width of the pool – 4 metres: