Using and abusing statistical information
Say you’re given some information showing some data about the average weight of a person based on their height, like this:
Sponsored Links
|
Height (cm) |
Average Weight (kg) |
|
150 |
56 |
|
160 |
63 |
|
170 |
68 |
|
180 |
78 |
|
190 |
87 |
|
200 |
96 |
Interpolation is all about finding out information about stuff between these data points. You can remember this by the ‘inter’ part of the word – ‘inter’ means ‘between’. For instance, if we wanted to find the average weight of a person who is 175 cm tall, we can’t get it straight out of the table. What we have to do is interpolate between the weight for a 170 cm tall person and a 180 cm tall person. The best way to do this is to first draw a graph of the data:
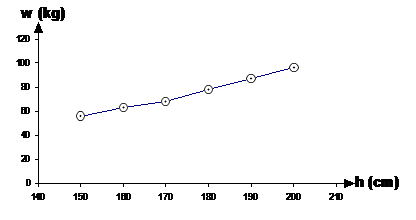
Now to work out what the average weight is for a 175 cm tall person, first trace a line vertically upwards from 175 cm on the height axis until it reaches the plotted line. Then trace horizontally across to the left until you hit the weight axis. The weight where your line touches the axis is the average weight of a 175 cm tall person:
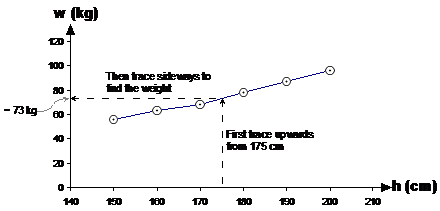
The interpolated weight we get from our graph is about 73 kg. Always check that this answer makes sense if you can. In this case, we have a weight value for 170 cm tall and 180 cm tall people. We’re interested in 175 cm tall people, so we’d expect the interpolated weight to be about halfway between the two weight values for 170 cm and 180 cm. 73 kg is exactly halfway between 68 kg and 78 kg, so our answer looks pretty good!

