The standard deviation is a very important way of measuring how spread out the values in a data set are.  It’s also more complicated to calculate than the measures covered before now.  You can think of it as sort of being like finding the mean deviation but with a square and also a square root thrown in.

The formal definition for the standard deviation, which I’m gonna call ‘SD’, is:

                            

If you calculate a standard deviation by hand, there are quite a few steps you need to go through:

·         Calculate the mean of the data set

·         Calculate all the deviations – how far each value is from the mean

·         Square all these deviations

·         Add up all these deviations

·         Divide this by one less than the number of values

·         Square root the value you get

Let’s do this for data set 2:

                                              12, 13, 14, 15, 15, 16, 17, 18

The mean of the data is 15.  I can tell this straight away because my two middle values are 15, and the values either side of them average out to 15 – the 14 and the 16 average to 15, the 13 and the 17 average to 15 and the 12 and the 18 average to 15.

The deviations and their squares:

Now, we’ve got 8 values in total, but we need to divide this sum by one less than the number of values we have – so 7:

                                                         

And now we just need to square root this value:

                                                           

So for data set 2, the standard deviation is 2.

Why do we divide by ‘n–1’?

This question bugged me for years and years and I heard lots and lots of answers for it.  Common sense would say once we’ve added up all the squares of the deviations, we just need to divide by the number of values to get the average squared deviation, before we square root it.  So why do we divide by one less than the number of values?

Here’s the explanation I formed in my head to explain it, it’s not a proof but it sort of makes sense:

When you’re working out the standard deviation of a data set you’ve got to remember you’re working with just a sample, not the entire population.  For instance, if you were working out the average age of a person when they bought their first car, you might ask 5 people – they would be a sample for the entire population:

                                           16.9, 17.3, 17.4, 17.6, 17.8 years

Now to work out the standard deviation, you need to first find the mean of the data.  This mean you calculate is the mean of the values in your sample, not the mean of the population.  So whilst the mean age of people when they first bought a car in your sample would be 17.4 years, the actual exact mean age that the entire population bought their first car at might be 17.9 years.  However you have no way of knowing this second statistic since you’ve got no way of asking every single person in the country.  So you just use the first mean calculated from your sample – 17.4 years.

The next step is to find the deviations – the differences between the values in your sample and the mean.  The mean you’re using has been calculated by averaging the values in your sample.  The differences between the sample values and your sample mean are going to be on average slightly smaller than the differences between the sample values and the population mean, because the sample mean is calculated from the sample values and hence is closer to them.

 

See how the deviations of the sample values from the sample mean are a lot smaller on average than the deviations of the sample values from the population mean?

The sample mean is an estimate of the population mean.  We’d really like to use the population mean in our calculation, but we can’t get that unfortunately.  Because we can’t survey the entire population, we are forced to use the sample mean as a ‘guess’ at the population mean.  Because the sample mean is calculated from the sample values, it is closer in value to the sample values than the population mean.  This means the deviations are going to be slightly smaller than they would be if we somehow knew the population mean and used it.  To compensate for this error, to find the average of the deviation squares, we can divide by a smaller number; ‘n – 1’ instead of ‘n’.  When you divide by a smaller number, you make the result bigger.  This makes our standard deviation answer a little larger and closer to what it would be if we knew the exact population mean.

Using your calculator to find statistical measures

Statistical measures such as the mean and standard deviation can be quickly calculated using special functions on your calculator.  Using a calculator is especially useful for something like the standard deviation, which requires so many steps to calculate.  With your calculator, all you have to do is enter in the data then press a few buttons and it will spit out the standard deviation for you.  I’ll use this simple data set to show how to do all the standard calculations using your calculator:

                                                          4, 7, 11, 8, 5

Changing into statistical mode

First thing you want to do is change the calculator into statistical mode.  Because there are only so many buttons you can fit onto a calculator, they have different modes you can run them in.  Some buttons have different meanings when the calculator is running in different modes.  Here’s how to change the two calculators into statistical mode:

Changing your calculator into statistical mode
Press the  button, you should then get a choice of modes.  Statistical mode is often abbreviated as ‘SD’ mode.  For this particular calculator, after pressing the mode button you need to press ‘2’.	Press the  button, this tells the calculator that we want to change modes. For this particular calculator, mode ‘3’ corresponds to statistical mode, so after pressing the mode button you need to press ‘3’.

Next thing you want to do is input the data values you have in your sample.  First of all though you want to remove any data values you’ve entered when you’ve been doing previous questions.  You can do this by clearing the statistical memory.  Here’s how to do it on the two calculators:

Clearing the statistical memory
If you look carefully at the  button, you’ll notice above it there is a  symbol.  This indicates that that you can use this button to clear the statistical memory.  Because the symbol is above the button, it means that this is a secondary function of the button.  To use it, we need to press the  button first. So to clear the statistical memory, first press the  button, then the  button, and then the  button.  This last button press gives the final go ahead to the calculator to go and delete all the data values currently stored in memory.	To clear the memory on this older style calculator, what you want to do is use the memory clear button - .  The actual function we want to access is the  part above the  button, so we need to use the  key. So to clear the statistical memory, press the  key followed by the  key.

Now we need to actually enter in the data values in our sample.  We can do this value by value:

Inputting the data
First type in the first value – ‘4’. Look at the  button carefully, just below it you’ll notice a  symbol – this is the data entry symbol.  This means in statistical mode we can use this button to enter data. So after typing in the value ‘4’, press the  button.  This stores the value ‘4’ in the statistical memory. Next, do the same thing for ‘7’ – enter in ‘7’ then press .  Repeat this for all the other data values. Some calculators such as this one have shortcuts for entering multiple values which are the same.  Say we wanted to enter in 10 lots of ‘6.0’.  We could do this two ways: Enter in ‘6.0’, and then press the  button 10 times.  This adds this value into memory 10 times. Or we could use this key combination: ‘6.0’, then , then , then ‘10’, and then finally .  This tells the calculator to add ‘10’ lots of ‘6.0’ to it’s memory.	First type in the first value – ‘4’. To actually add this data value into the statistical memory, press the  button.  This adds the value on the display into the statistical memory.  Repeat this process for all the other data values – enter the data value in first then press the  button. If you have lots of identical data values, just enter the data value once, then press the  button as many times as there are the same data value.  So say you had 21 data values equalling 6.3.  You’d do this: Enter in ‘6.3’ Press the  button 21 times.

Now that we’ve entered the data into our calculators, we want to find out useful statistical information about it. 

Finding statistical information
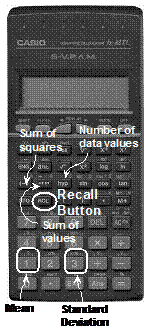
The recall button is used in combination with the ,  and  buttons to get the sum of the values, the sum of the squares of the values and the number of data values. These buttons are really used not because of their main label, but the ‘A’, ‘B’ and ‘C’ labels above them.   The mean and the standard deviation are calculated using the  button. Sum of Values Press the  button, then the  button. Number of Data Values Press the  button, then the  button. Sum of Squares Press the  button, then the  button. Mean Press the  button, then the  button, and then finally the  button. Standard Deviation Press the  button, then the  button, and then finally the  button.	Some of the buttons on this calculator actually have three different effects, depending on what mode you’re in and what buttons you press beforehand.    The label on the button itself –  in this case) shows what happens when you press it without pressing any special buttons before it.  The label in the square brackets above the button -  in this case – shows what happens when you press the button after pressing the  button.  The legend along the top of the calculator shows what happens when you press certain buttons after you press the  button. The mean and standard deviation are accessed using the  button. The sum of values, sum of squares, and number of values are accessed using the  button. Sum of Values Press the  button, then the  button. Number of Data Values Press the  button, then the  button. Sum of Squares Press the  button, then the   button. Mean Press the  button, then the  button. Standard Deviation Press the  button, then the  button.