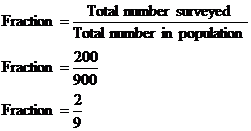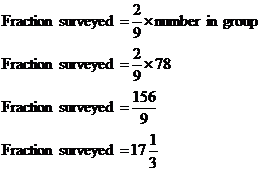Statistics

When a company wants to do market research for a proposed new product, they can’t go around and ask every single person in the world or country questions.  Occasionally this does happen – for instance a government may do a population census, where they survey everyone.  But usually, for practical reasons such as time and cost, you pick a sample of people whose opinions will hopefully represent what people in general would think.

It’s very, very important to go about picking the people in your sample in the correct way.  For interest, say a radio station was doing a survey to see what the most common surname was in a city, by asking people in public what their surname was.  They would need to pick a representative sample of the population.  Possible ways they could get it wrong would be doing the entire survey in Chinatown, or an Italian or Greek district of town, when the majority of suburbs were mostly occupied by Australians of other nationalities.  They might get a misrepresentative idea of what the most common surname was.

A sample must fulfil two basic requirements:

·         It must be large enough to give a good representation of the entire population

·         It must be small enough to be practical in terms of costs etc…

There are a few types of sampling that you can do.  But first we need to define a couple of terms:

·         Population – the whole group of things that we are surveying

·         Item – an individual thing within the population

·         Sample – the group of items we have selected from the population to represent the population.

Here is a description of the sampling types:

Simple random sampling

In random sampling, all items in the population (for instance all people in the population of a country) have an equal chance of being included in the sample.  The most common example used to illustrate simple random sampling is the phone book example.  If you had a phonebook with everyone’s name in it, you could get a simple random sample of say 100 people by turning to 100 pages at random and picking a name from the page with your eyes shut.

Systematic or interval sampling

In this type of sampling, you pick items at regular intervals from the population to make up your sample.  This type of sampling is good for situations like testing products in a factory production line, where the equipment may work for a while but then start malfunctioning.  For instance, a factory worker might test every 100^th item coming off a conveyer belt.  By testing at regular intervals, you are more likely to pick up the malfunction.  If you just picked one batch of products at one time, you might completely miss the error.

It’s also good for if you were asking people in a shopping mall about something like unemployment.  If your whole sample came from people at midday during a weekday, you might get a misrepresentative set of opinions about unemployment, since a lot of people who did have jobs would be at work.  You would probably be better off doing systematic sampling, where you asked a certain number of people every day of the week, including weekends.

Stratified sampling

Even with interval sampling, you might still miss out on representing the opinions of everyone in the population.  For instance, if you did a survey at night by calling up people at home about what type of job they did, you would be leaving out all the night shift workers.  In stratified sampling, you first split the population up into groups or categories.

Say you were doing a survey in Australia asking people which state they thought was the ‘best’.  To make it a truly representative survey, you might group people in the population depending on how old they were.  Then, from each age group, you could randomly select a certain number of people.  The number of people you would need to select from each age group would vary.  For instance, to give a good representation of the entire population, you would need to select a lot more people in the 20 – 30 year old group than from the 90 – 100 year old group, since there are a lot more 20 – 30 year olds in the population.

Cluster sampling

Cluster sampling involves splitting the population up into groups or clusters.  Then, some of the clusters are picked at random, and every single item within these selected clusters is used in the sample.  For instance, if you were trying to find out people’s opinion on a particular washing product, you might split a city up into clusters based on their suburb, there might be 100 clusters in a medium size city.  Now, it would be expensive to travel around to every single suburb in that city and ask people their opinions.  Instead, you could use cluster sampling and select 5 of these clusters at random, and then try and ask everyone in each of the suburbs. 

Cluster sampling is different to stratified sampling.  In stratified sampling, the population is split up into groups and then a certain number of items from every group are selected at random.  In cluster sampling, the population is also split up into groups, but then only a few of these groups are selected at random and then every item from within those selected groups is used.

Stratified sampling question

A fashion company is coming out with a revolutionary line of clothes for teenagers, and wants to know whether they like them or not.  So they send you to the local school to do a survey on the students.  There are a total of 900 students in the school, but you only have time to interview about 200.  So that you get a good representation of what students of all ages and sexes like or don’t like, you decide to do use a stratified sampling technique.  How many students should you select from each group?   Grade Male Female     8 78 91     9 81 87     10 82 88     11 95 101     12 93 104

Solution

Well, the students have been split up in two different ways – by their sex, and also by what grade they are.  There are two sexes – male or female, and 5 grades, so combined this creates 10 groups of students.  Now, because we have only time to survey 200 out of the 900 students, we’re only going to be interested in a fraction of the students in each group.  What we want to do is work out the size of this fraction. In this case, it’s pretty easy – the fraction for each group is the same as the fraction for the entire school – 200 out of 900 students:                                    We can use this fraction to work out how many students should be surveyed in each group, by multiplying the number of students in the group by the fraction.  For example, grade 8 male students:                                   Now because we can only survey a whole number of students, we need to round to the nearest integer – 17 in this case.  So we need to select at random 17 students from the male grade 8 group.  We can do the same thing for the other 9 groups, to get a table telling us how many to survey in each group: Number surveyed Grade Male Female 8 17 20 9 18 19 10 18 20 11 21 22 12 21 23 Now because for each group you are rounding to the nearest integer, it is possible for the total number of students surveyed to be very slightly different to how many you intended.  In this case, if you add up how many students are to be surveyed in each group, it comes to 199, 1 less than how many was said in the question.  This slight difference won’t have a bad affect on the survey however – it’s better to get your proportions right than to arbitrarily tack on one extra student in a group to make up the total exactly.