Scientific notation is an efficient way of writing numbers, especially very large or very small numbers. For instance, this is a normal number and what it looks like in scientific notation or standard form:
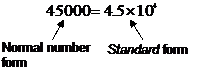
Sponsored Links
When you do calculations with numbers in standard form, you can often work with each part of the number separately. For instance, if we had to calculate:
![]()
We can do this in two separate parts – we can multiply the decimal numbers together first, then multiply the powers of 10 together. At the end of all this we can combine the two parts by multiplying them together:
|
|
|
|
Decimal part
|
Power part
|
Now we can recombine these two parts:
![]()
Now, normally you write the decimal number as a number in the range 1 to 9.999…, at the moment our decimal number is larger than this – ‘22.72’. What we can do is reduce the size of our decimal number by a factor of ten, and increase the index of our power of 10 by one. What we’re doing really is multiplying one part of it by 10, and dividing another part of it by 10. This leaves the overall number unchanged:
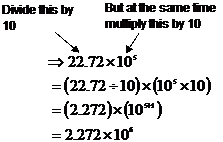
Dividing is the same, say we had to do something like this:
![]()
Once again we can do the calculation in two separate parts:
|
|
|
|
Decimal part
|
Power part
|
And finally recombine them:
![]()
Our decimal number is smaller than one, so let’s multiply it by a factor of 10. Because we’re increasing the size of our decimal number, we have to decrease the size of our power of 10 – we can do this by reducing the index by one:
![]()
Adding and subtracting numbers in scientific notation
When you add or subtract numbers that are written in scientific notation, you need to first get them all multiplying the same power of 10. So say I had to calculate this:
![]()
It’s easiest to try and make all the terms have the same power of 10 as the lowest power of 10. In this expression, the lowest power of 10 is 10 to the power 2. So we have to change the 103 into a 102. Because we’re dividing the 103 by 10, we need to multiply the decimal number in front of it by 10 to keep the same overall number:
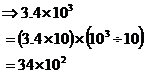
Now we can do our subtraction, by subtracting the decimal numbers:
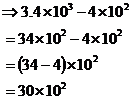
Because ‘30’ is not in the standard 1 – 9.999… range, let’s divide it by 10 and multiply the power of 10 by 10:
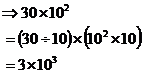
If you look at the original question, and convert the numbers out of scientific form, you get:
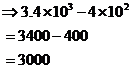
This matches with the answer we calculated using scientific notation.

