Burke and Wills question

Burke and Wills were two famous Australian explorers who did many fantastic journeys into inner Australia.  On 21^st April, 1861, they were in a very bad way, and managed to struggle back to a base camp, but found no-one.  However, they found a note cut into a tree which told them that a backup team had just left the camp earlier that day.  They did not decide to try and chase them, and ended up both dying a few months later.  Let’s imagine the backup team left at 10 am that morning, travelling at 2.5 km / hr back to civilisation.  If Burke and Wills had pursued them, they would have started at 5 pm that night.  Because of their weak state, they could only manage 5 km / hr, and only for 8 hours until they collapsed from exhaustion.

·         Write two equations for the distance travelled from the camp by both groups ‘t’ hours after 5 pm.  What is the ‘unknown’?

·         On the same set of axes plot graphs showing the pursuit, using ‘t’ as the x-axis and distance from the camp as the y-axis.  Use the graph to work out whether Burke and Wills would have caught up in time.

·         Use the equations to get the answer as well.  If they catch up, how far are they from the camp?

Solution

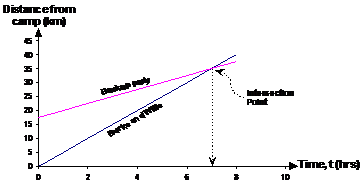
The equation for Burke and Will’s distance from the camp after 5 pm is easy, it’s just:

The extra  bit tells us that this equation is only valid when t is smaller or equal to 8.  This represents the information in the question telling us they’ll collapse after 8 hours.

The equation for the backup party’s distance from base camp has to represent the fact that they’ve been travelling for 7 hours before 5 pm.  In 7 hours they have travelled 17.5 kms, so we need a “+ 17.5 km” part in our equation:

Lots of questions ask you what the unknown is.  Think about the question, and what you’re trying to find out.  For instance, in this question we’re interested in whether Burke and Wills will catch the backup party.  We have these variables – d_{Burke and Wills}, d_{backup party} and t.  These are all initially unknowns, since we don’t know the value of any of them at the start.

The plot for the graphs is easy, they’re just two straight lines.  The Burke and Will’s plot will start from the origin, but the backup party’s line will start some way up the distance axis to represent the fact they’re already 17.5 km from the camp at 5 pm.  Now, how far ahead in time do we need to plot the graph?  Well, Burke and Will’s time is up after 8 hours, so our time axis should only go for 8 hours:

Looking at the graph, the lines cross over each other around the 7 hour mark.  This cross over point represents the point in time when both groups are the same distance from the camp.  Assuming that Burke and Wills follow exactly the same path as the backup party, they will have caught up with them 7 hours after B & W first set out from camp.  Just within their time limit.

Now let’s solve this problem using the equations.  We know that if B & W could continue at their speed for ever, they would definitely catch the backup party, since they’re travelling faster than them.  We want to know however if it would take more or less than 8 hrs, since if it would take more, then they wouldn’t catch them before collapsing from exhaustion.  The catch-up point is the point when both groups are the same distance from the camp.

For the catch-up point:

This means we can equate our two equations, like this:

Now we have one unknown value – the time ‘t’.  We’ve got rid of the other two unknowns, d_{Burke and Wills} and d_{backup party}.  We can easily solve for ‘t’:

Great, we get the same answer as we did using our graphs.  Burke and Wills will catch up with the backup party 7 hours after 5 pm, or at midnight.  Don’t forget the very last bit of the question – working out how far from the camp they all are.  Just use one of the distance equations and substitute this value of ‘t’ into them: