Trip graphs

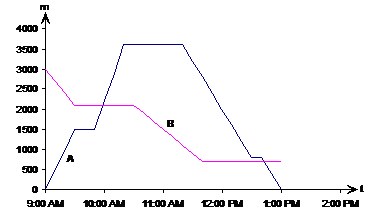
One type of graph you may come across is one showing the distance travelled during a journey by foot or by car. There are a large number of questions you can be asked about these graphs, so there are often a large number of marks at stake. If you can quickly answer the questions, then you can get a lot of marks, plus you can move on to other harder questions in the exam. Take this graph for instance. Bob and Wendy live on the same road, which also has some shops and a pub on it. The graph shows Wendy’s walk to the pub and back, and also Bob’s trip out to the local shops. The distance on the y-axis is the distance from Wendy’s place along the road.

Sponsored Links

Here are some of the typical questions you might be asked and how to solve them:

Which line represents Wendy’s journey to the pub?

The lines are only labelled A and B, but there is no indication of which one is Bob’s and which one is Wendy’s. One line starts at 0 metres, the other starts at 3000 metres. If we look at the question, we read that the distance on the y-axis represents the distance from Wendy’s place. Wendy starts at her place, which must mean she starts at 0 metres from her place. So that means she is line A.

How far is Bob’s place from Wendy’s place?

For this type of question we’re looking for a distance answer – the distance between two points on the graph. First of all, we’ve got to work out where these two points are on the graph. First up, Wendy’s place. In the question, it says that the distance on the y-axis is the distance from Wendy’s place. From this we can work out that Wendy’s place corresponds to the ‘0 m’ distance on the y-axis. What about Bob’s place? Well, Bob is represented by line B. Bob starts at home, so his house must be located at the 3000 metre point, since that’s where his line starts. So it’s a simple calculation to find the distance between their two houses:

At 11 am what speed is Bob walking at?

Speed is the rate at which you cover distance, for instance in a car you might be travelling at 50 km / hr down a suburban street. When you’re walking, speeds are more like 3 – 6 km / hr though. To work out how fast someone is walking you need to work out the gradient of the graph. We want the gradient of Bob’s line at 11 am:

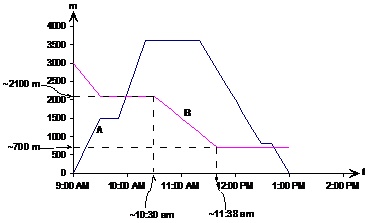
We can use the whole straight segment of Bob’s line around 11 am to work out the gradient:

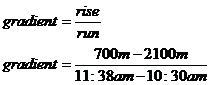
When you subtract one time from another, the answer is given in units of time rather than as an actual time. In this case minutes are probably most suitable:

Now, units of ‘metres per minute’ aren’t normally used, let’s convert it to something more standard – km / hr. First we can convert to ‘metres per hour’:

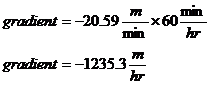
Then we can convert to ‘metres per kilometre’:

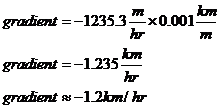
Now what does the ‘negative’ mean in this case? Well, it doesn’t mean that Bob’s walking slower than 0 km / hr! All it means is that he’s walking towards Wendy’s house at 11 am. So a good answer would be something like:

Bob is walking at a speed of 1.2 km / hr at 11 am.

What was Wendy’s average speed from 9 am to 1 pm?

Average speed over a time interval can be calculated just by looking at the total distance covered, and dividing it by the total time. Walking to the pub, Wendy covers a distance of about 3600 metres. Then she walks all the way home, another 3600 metres. The horizontal bits in her line don’t add to her distance at all – they’re times when she’s not actually walking. So her total distance is 7200 metres. The total time is 4 hrs from 9 am to 1 pm. So:

At what times did they pass each other?

This one’s easy – just look for the points on the graph where the two lines cross over:

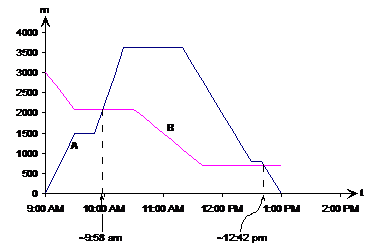
Looks like they pass each other twice, once around 9:58 am and again around 12:42 pm.