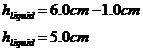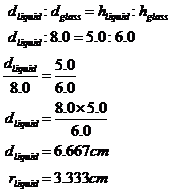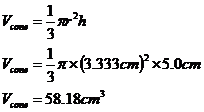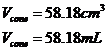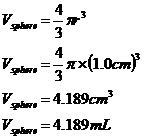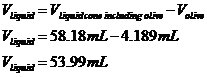Volumes and Areas of More Complicated Shapes

The volumes and areas of solids like spheres or cones are a bit more complicated to work out than say for a cube.

The sphere

A sphere is a perfectly round object like a ball. It has only one surface, which is curved, and no corners or edges.

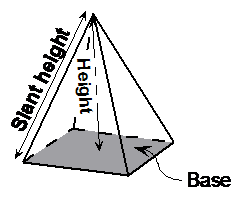
Pyramids actually have two different heights. The slant height is the distance along one of the edges from the base to the pointy tip – it’s ‘slant’ because it’s at an angle to the vertical. The vertical height, usually just called the height, is the vertical distance from the centre of the base to the tip, and is shorter than the slant height. Usually ‘h’ is used to represent the vertical height, and ‘s’ to represent the slant height.

If you make a prism which has the exact same base as the pyramid and the same height, then it has a volume three times as great. This is where the formula for the volume of a pyramid comes from:

Remembering the one third volume fact about the pyramid is a good way of remembering the formula – it’s just one third the volume of a prism with the same base and height.

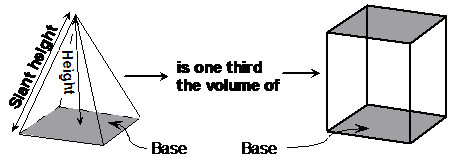
Proving the volume of a pyramid formula

Here’s a way to show how to get to this formula using geometry. What we want to do is represent a pyramid by a series of levels. Say we’re trying to represent a square based pyramid, we can build up one by using thin square based prisms:

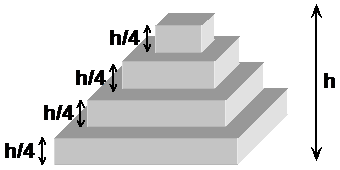
Now, the volume of this ‘pyramid’ is made up of the volumes of each layer. The volume of each layer can be calculated by multiplying its height (h / 4) by its cross sectional area:

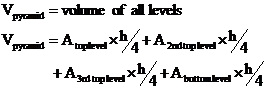
There are four levels in our diagram, and the side length of each level decreases by a regular amount as you go up each level. The second bottom level’s side is three quarters the length of the bottom level. The third level’s side is only half as long as the bottom level. The top level has a side only one quarter the length of the bottom level’s side. The side lengths decrease in quarter amounts because we have four levels.

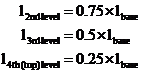
How does the area change as we go up levels? Well, area is a two-dimensional quantity, so it will decrease at a faster rate than the side length. Here’s the calculation for the area of the 2^nd bottom level:

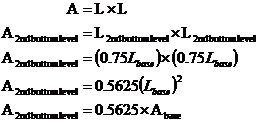
So in general, the side length and area of any level depends on how high up in the pyramid it is and on how many levels there are in total.

Now, this four level pyramid doesn’t really look much like a real pyramid, it’s too chunky. However, if we use lots and lots of levels, it starts to look just like a real pyramid:

If we use ‘N’ number of levels, then the height of each level is going to be . Now, we can number the levels from 1 to N, starting at the top of the pyramid. For a pyramid with N levels, the side length of level number ‘i’ is (if the top level counts as level number 1):

So the area of level ‘i’ is going to be:

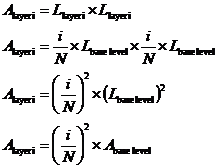
We can get the volume of this pyramid by starting at the top and adding up the volumes of each layer:

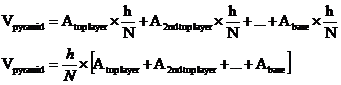
I have factorised out the part from each term. Now, what about those areas? Well, we can substitute our formula for the area of layer number ‘i’ into this equation:

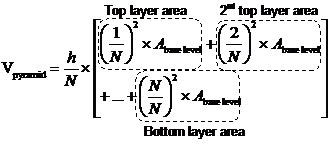
Because we have an ‘A_base’ in every term inside the square brackets, we can factorise it outside as well:

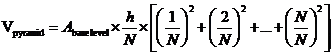
Now we know that our final formula for the volume of a pyramid has ‘A’s in it and ‘h’s in it, so that’s fine, but it doesn’t have any ‘N’s in it. Let’s group these together and try and get rid of them. First we can change how the inside of the bracket looks, then we can bring the ‘one on N’ in from outside the brackets:

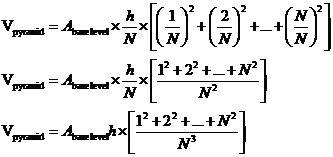
Now, what does 1² + 2² + … N² equal? Well, there is a formula which tells you the sum of any series of square numbers from 1 to N:

There is a way to prove this formula as well, but I won’t go into it here. You can satisfy yourself that it works by trying it out.

We can use this formula to replace the 1² + 2² + … N² line in our equation:

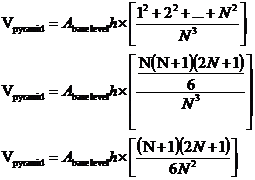
Now we can expand out the top line of the fraction and simplify it:

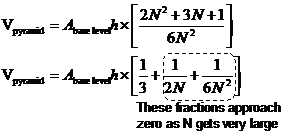
Now, the more layers we have in our pyramid, the closer it looks to an actual pyramid. So as we make pyramids with more and more layers, N becomes a very large number (since N is how many layers there are). When N becomes a very, very large number, two of the three fractions inside the brackets become very small numbers, since N is in their denominators only. As N becomes even larger these two fractions eventually become zero, and we’re just left with the one third:

There’s our proof! Although we proved it for a square based pyramid, it applies to any pyramid, because the cross sectional areas would change as you moved through the pyramid in exactly the same way, regardless of what shape the area was. You’d never be expected to actually come up with a proof like this yourself in an exam, but it is good to at least understand how it works.

The surface area of a pyramid is calculated by just adding up the areas of all the sides and the base:

There’s always one base, and then as many triangular sides as there are sides on the base. Calculating the base area can be a little tricky, especially if it’s something like a decagon (10 sided shape). To work out the area of the triangular sides, you need to use the triangle area formula:

Be careful! The ‘h’ in this equation is not the slant height or the vertical pyramid height. It’s the height shown in the diagram:

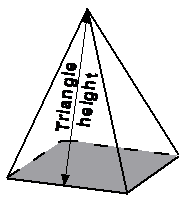
So if you’re only given the slant height or the vertical pyramid height, you’ll need to use Pythagoras’ Theorem to get the actual triangle height. For instance, if you had a square based pyramid, and you only knew the square side length and the pyramid’s vertical height, you could work out the triangle height like this:

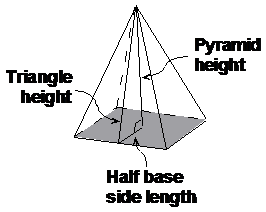
Notice how the triangle height line, the pyramid height line and the ‘half base side length’ line together form a right-angled triangle? This means we can use Pythagoras’ Theorem:

If the base of your pyramid isn’t a regular shape like a square or hexagon, then you’re going to have different size triangular sides. This means you’ll have to work out the area individually for each triangle. For symmetrical pyramids like a square based pyramid though, you only need to work out the area of one triangular side, then multiply it by however many there are.

The cone

The cone is like a pyramid except with a circular base. It has two heights like a pyramid – a slant height and a vertical height, normally just called the ‘height’.

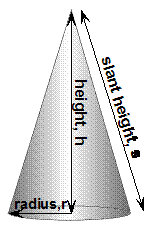
A pyramid’s volume is one third the volume of a prism having the same base and height. Well, the volume of a cone is one third the volume of a cylinder which has the same base and height:

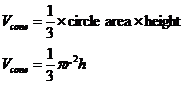
You can actually work out the formula for the surface area of a cone by imagining unwrapping the cone to form its net (the flat shape that you fold together to get the solid shape):

So the surface area of a cone is made up of two areas – the area of the circular base, which is easy to calculate, and the area of the curved side. The area of the circle is just . The other area is just a sector of a circle. The arc length of the sector is just , since we need it to join up with every point on our base circle. So the fraction that the sector is of the entire dotted circle is its arc length divided by the circumference of the dotted circle:

This means that the area of the sector is just this fraction of the area of the dotted circle:

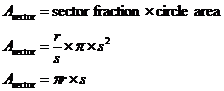
The total surface area of the cone is:

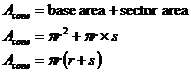
Now, if you don’t have the slant height of the cone, you can calculate it from the vertical height and the base radius using Pythagoras’ Theorem:

Cone nets look different depending on how ‘tall’ the cone is compared to the radius of its base. If we have a cone with a base radius ‘r’, and a slant height ‘s’, then we can calculate the angle θ of the sector because we know the length of the sector arc has to be long.

Now here when we’re talking about a circle we mean the large dotted one in the diagram. The small circle that is the bottom of the cone is referred to as the ‘base’. So we have two radii – r_base and r_circle. Now r_circle is just the slant height of the cone, so we can replace it and rearrange the equation like this:

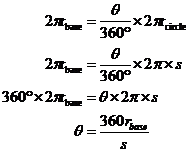
So say I wanted to draw the net for a cone that had a base radius of 1 and a slant height of 8. I could work out the angle of the sector using this formula:

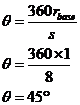
So the net would look something like this:

Notice how the sector or wedge is a lot narrower than the first cone net we looked at, this is because the slant height to base radius ratio is a lot larger – the cone is a lot taller and skinnier.

Martini glass question

A martini is a very famous alcoholic drink which Mr James Bond is in the habit of ordering – “shaken, not stirred” being a classic quote. It’s served in a conical glass, with an olive in it.

Mr James Bond is arguing with Mrs Bond over how much liquid there is in his Martini glass. Mr Bond guesses 40 mL. Mrs Bond thinks it’s more like 55 mL. The liquid is filled to within a centimetre of the top of the glass, which has a diameter of 8 cm. The height of the conical part of the glass is 6 cm (assume the top of the glass is like an upside down cone). The olive is spherical and has a diameter of 2 cm. How much liquid is there in the glass?

Solution

This is quite a tricky question, because you aren’t given the exact information you need. We want to work out how much liquid there is in the glass including the volume that the olive takes up, and then subtract the volume of the olive. The liquid in the glass forms an upside down cone shape. We have the total height of the conical section, but to calculate the volume of liquid we only want the height of the liquid. You also have the radius of the very top of the glass, but we want the radius of the top part of the liquid.

So, the height of the liquid is easy to work out – it’s just one centimetre less than the overall height of the conical part:

We also need to know the radius of the top of the liquid part. This is a bit trickier to work out, we need to use ratios to help us. What we’re doing is comparing the conical part of the glass with the conical section of liquid inside it:

We can write a ratio comparing the two diameters and the two heights:

Now we can work out the volume of the liquid inside the glass, including the olive:

Now 1 cubic centimetre of fluid is the same as 1 millilitre (mL) of fluid:

We however want the volume of liquid inside the glass, not including the olive as part of the volume. The volume of the olive is:

So we just subtract this from our total liquid volume:

Looks like Mrs Bond is much better at estimating volumes than Mr Bond! Oh well, he can’t be good at everything.