Parabolic Inequations And Finite Differences

A normal parabola should be quite familiar to everyone.  For instance, check out this quadratic function and its graph:

                                                     

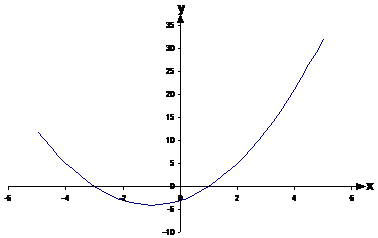
Parabolic inequations are all about finding the values of ‘x’ (or whatever is plotted on the horizontal axis) that satisfy (make true) an inequation, like this one:

                                                      

Notice how this is similar to the quadratic function we just plotted, except with a larger than or equal sign and a number on the other side of it instead of a ‘y’.

What we’re looking for is parts of the graph which are larger than or equal to ‘5’, in the ‘y’ direction:

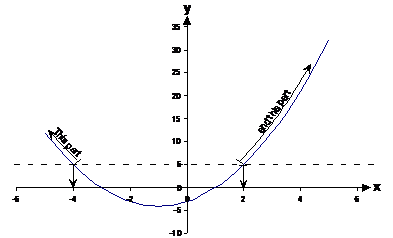
There are two sections of the graph that are larger than or equal to 5 in the y direction – the part for x values smaller than or equal to ‘–4’, and the part for x values larger than or equal to ‘2’.  In mathematical set notation our answer would be:

                                               

Remember the ‘U’ symbol is the union symbol – in this situation it means the solution is, “all the x values smaller than or equal to –4 and all the x values larger than or equal to 2.”

Solving it analytically

You can also solve it by manipulating the inequation.  If we moved the entire line 5 downwards, then the x-axis intercepts would be the points at which our solutions started.  This is the same thing as taking 5 away from both sides of the inequation:

                                                

Now we’ve got a new inequation we’re trying to solve, with ‘0’ on one side.  If we solve the equivalent equation, we can work out the points at which  equals 0:

For :

                                             

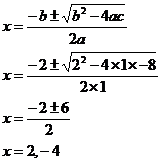
So our graph would cross through the x-axis at ‘2’ and ‘–4’.  Now because the ‘a’ coefficient is positive (+1), this means the graph is a valley-like graph, with a minimum.  This minimum has to be located somewhere between  and .  This means as we travel outwards from this minimum through ‘–4’ and ‘2’ on the x-axis, our line is going to go from below the x-axis to above the x-axis.  We’re looking for values larger than or equal to ‘0’, so this means we want the values from  outwards in the negative direction, and from  outwards in the positive direction.  So in other words, we get our previous answer again:

                                               

This graph summarises what we have done:

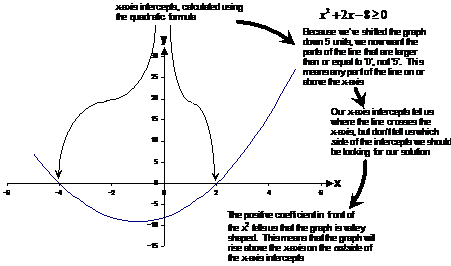
So the general analytical solution is to:

·         Modify the inequation so that there is a ‘0’ on one side, by adding or subtracting an amount

·         Solve for the x-axis intercepts of this new inequation, treating it as if it was an equation.

·         Look at the coefficient in front of the squared term.  If it’s positive, the graph is a valley type graph.  This means that the line goes positive as you move outwards through the x-axis intercepts.  If the coefficient is negative, the graph is a hill type graph.  This means the line goes positive as you move inwards through the x-axis intercepts.

·         Work out where your solution is based on the last step and whether you’ve got  symbols, or  symbols.

The last step might require some explaining.  Say I have an inequation like .  The coefficient in front of my  term is negative.  Where do I look for my solutions once I’ve found my x-axis intercepts?

Well, the negative coefficient means it’s a hill type graph.  This means that as I move outwards through my x-axis intercepts the line will be going negative.  I’m interested in the parts of the graph that are smaller than 0, or negative, so that’s where I search for my solution – outwards in the positive and negative directions of my two x-axis intercepts.  Also, because it’s just a ‘smaller than’, not ‘smaller than or equal to’ symbol, my answer’s going to be something like this:

                 

Note the larger than symbols (not larger than or equal to).