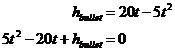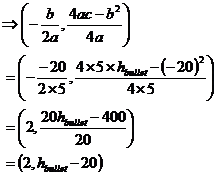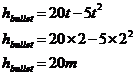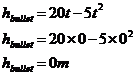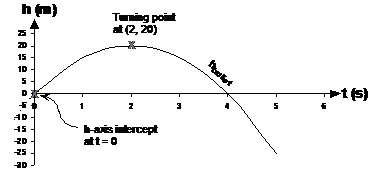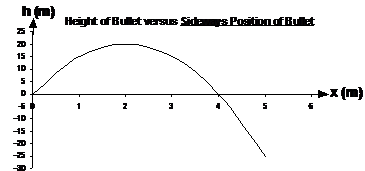Using A Graph

Solution

Using a graph, we don’t need to solve the simultaneous equations algebraically.  Instead, we can just graph the two equations on the same set of axes.  Both equations are written in the form, “height = something…”  This means that where the two lines cross over each other, the heights are the same.  This means we can read the answer straight off the graph.  So first let’s plot them.

The linear equation is easy to plot, it’s just a straight line starting at the origin and sloping upwards to the right.  The parabola representing the bullet’s height is a bit more complicated.  First we need to write the equation in standard form:

Now, instead of ‘x’s, we have ‘t’s, so let’s rewrite this standard quadratic form:

Our equation for the bullet’s height is .  We can rearrange this into the standard form:

So this means a = 5, b = –20 and c = h_bullet.  We can substitute these into our expression for the turning point coordinates:

Notice how we only have a numerical value for one of the turning point coordinates – the ‘x’ coordinate, or for this particular question, the ‘t’ coordinate.  However, we can work out what the ‘y’ value, or for this particular question, the ‘h’ coordinate is, by substituting t = 2 into our bullet height equation:

So the coordinates of the turning point in the graph are (2 s, 20 m).  The other thing we need to do is work out our ‘y’ axis intercept – in this case it’s our ‘h’ axis intercept.  This occurs when our ‘x’ value is equal to ‘0’ – in this question when our ‘t’ value is equal to ‘0’:

So our ‘h’ axis intercept is at 0 m.  This makes sense – at time 0, just as Jason fires the rifle, the bullet hasn’t travelled anywhere – so we’d expect it to be 0 metres above Jason.  So now we have the turning point coordinates and the h-axis intercept, we can plot the parabola:

The part of the parabola below the t-axis doesn’t really need to be there – it indicates that after 4 seconds the bullet will have fallen past Jason and be going below him.  Most likely in real life it will have hit the ground and stopped.  I’ve continued the parabola below the t-axis just to give a better overall idea of its shape.

Don’t be tricked by the shape of the parabola – it looks like we’ve plotted a graph showing the parabolic path of a bullet if we fired a rifle at an angle.  But we haven’t - we have plotted time on the horizontal axis, not the bullet’s sideways position.  So if you follow along the parabola line from left to right, you’re following the bullet’s vertical height (h) as time (t) increases.  The graph shown next is a completely different graph not from this question. It shows a bullet’s vertical (h for height) and horizontal (x) position, but does not have time.  Make sure you understand exactly what a graph is showing.  A common mistake is to recognise a characteristic shape in the graph (such as a parabola) and jump to a conclusion about what the graph is showing.  Instead, look at what the two axes are, and think about exactly what the graph is telling you.

So back to our first graph, showing the vertical height of the bullet plotted as a function of time.  We must not forget to plot the line showing the balloon’s height above the ground as well.  This one’s easy to plot since it’s a straight line, so we can quickly add it to the graph:

Now, when the lines touch and cross over each other, we know at that time the bullet and the balloon are at exactly the same height.  This happens at two times in the graph – at time t = 0, and at around time t = 3.6 seconds.  Let’s drop a vertical line from the 2^nd cross-over point and work out where it crosses the t-axis:

It looks like the cross-over point is at around t = 3.6 seconds.  We can also read off the height of the bullet and the balloon at that time by reading the value of ‘h’ at that time.  From the graph it looks like h is around 7.5 metres.

Now is the bullet travelling upwards or downwards at this time?  Well, the parabola is sloping downwards at this point, which means that the value of ‘h’ is decreasing as time passes.  This means that the bullet is heading downwards.

Comparing our graph answers with our algebraic answers, our time answers are exactly the same, but our height answers are a little bit different, caused by the inexactness of the graph.