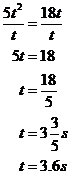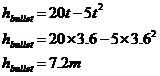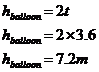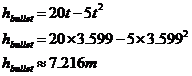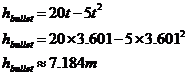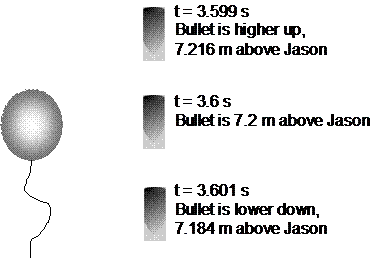Some of the more complicated questions will ask you to solve simultaneous equations, where one equation is a linear one, but the other is a quadratic one. You can do this in two ways – you can try and solve it algebraically, or by graphing. Sometimes the question will specifically ask you to use one of these methods. Here’s a sample question where we’ll work through both types of solution:
|
Sponsored Links |
||||
|
Jason has a helium balloon and an air rifle. He lets go of the balloon and fires the rifle straight up in the air at exactly the same time. The balloon rises at a steady rate – it rises 2 metres every second. The height of the bullet in metres above Jason after ‘t’ seconds is given by this equation: When the balloon and the bullet are at the same height, what is that height? Is the bullet on its way up or down? |
||||
|
Solution |
||||
|
So the question is asking for a height as an answer – how high above Jason the balloon and the bullet are when they are at the same height as each other. Now obviously, just at the moment Jason shoots and releases the balloon, they are at the same height. But after this, the bullet initially is going to be a lot faster and get a lot higher than the balloon. But gravity’s eventually gonna catch up with it and slow it down until it falls back down to earth. The balloon’s gonna keep going up however. So they’re both going to be at the same height at some later point in time. We’ve got an equation which describes how high above Jason the bullet is after time ‘t’. It would be nice to have an equation which told us how high above Jason the balloon was after time ‘t’. We know it rises steadily, so it’s going to be a linear equation, like this: Now we have two equations. We’re interested in the height of the balloon and the bullet when they’re at the same height. So we can equate their heights, and simplify the equations: Now we’ve got a quadratic equation. We can simplify it a little: Now, one value of ‘t’ that would make this equation true is of course, t = 0. This corresponds to the fact the balloon and the bullet are at the same height above Jason at the instant he lets go of the balloon and fires the rifle. So that’s one solution for t. However, we can also divide both sides of our equation by ‘t’, like this: Bingo! We have worked out that as well as being at the same height after ‘0’ seconds, the balloon and the bullet are also at the same height above Jason after 3.6 seconds. This isn’t what our question wants however – it’s interested in how high above Jason they are at that time. What we can do is substitute this value of ‘t’ into one of the two original equations, either one will do:
Not surprisingly, we get the same height whichever equation we use – if we didn’t, we’d have to go back and check all our calculations! Now, how do we work out whether the bullet is travelling upwards at this stage or downwards? Well, one way is to find out the height of the bullet a tiny bit earlier in time than 3.6 seconds, say at 3.599 seconds, and also a tiny bit later, say 3.601 seconds:
So just before 3.6 seconds, the bullet’s higher up, and just afterwards the bullet is lower down. This indicates that the bullet is on its way down when it passes the balloon.
|