Quadratic equations

In first degree equations the maximum power any variable or pronumeral is raised to is ‘1’. In second degree equations, the maximum power that any variable or pronumeral is raised to is ‘2’. Quadratic equations are second degree equations which always have a variable raised to the power ‘2’.

is a quadratic equation, because ‘x’ is a variable and it’s raised to the power ‘2’. It could also be written .

Section 1.1 - Quadratics with Only a Squared Term and a Number

There are many different types of quadratic equations. The simplest ones have only a term with the variable squared in it, and also another number term, like this:

Now, it’s pretty simple to solve this, we just need to take the square root of both sides:

However, there are actually always two answers to a quadratic equation. We’ve just found one solution. But what about if x was equal to negative three?

If then:

So if you put a value of into the quadratic equation, it also makes it true. This is because when you multiply two negative numbers together, you always get a positive number.

So when you get to the square rooting stage in a quadratic equation problem, you can use a symbol in front of the square root sign to indicate that you’re finding both the ‘plus’ and the ‘minus’ solution:

So now our answer is saying that x can equal ‘3’ or ‘–3’.

Only one answer to the square root of a number by itself

Be careful though, there is only one answer when you take the square root of a number just by itself:

You only get the two ‘plus’ and ‘minus’ answers when you’ve got the square of a variable involved, and you need to take the square root of both sides, like this:

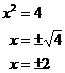
You can complicate this type of equation a little bit more if there is a coefficient in front of the squared variable term:

Then you need to divide both sides by the coefficient before you do the square root:

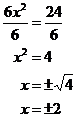
And you won’t always get a whole number answer, like in this case:

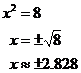
Sometimes you’ll end up trying to find the square root of a negative number, like in this case:

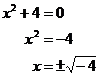
Now, based on our current knowledge, there is no number that you can multiply by itself to give a negative number. A positive number multiplied by itself will give you a positive answer. But a negative number multiplied by itself will also give you a positive answer. This means that there is no way we can work out what the square root of a negative number is. So there is no solution to this quadratic equation. In grades 11 and 12 in advanced mathematics you may cover a way to solve this equation, but no need to worry about that now.

You could however simplify it a little bit if you wanted, remembering that you can split square roots up like this:

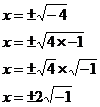
Quadratics with a power 1 term but no number only term

A slightly more complicated quadratic equation is one where you have both a squared term and a term where the variable is raised just to the power 1, but no number only term, like this:

You can solve these types of quadratic equations by factorising them. For instance, in this equation all terms have a common factor of ‘x’, so we factorise it like this:

Now, the trick here is to remember that when you multiply anything by zero, your answer is zero. This means that either the ‘x’ outside the brackets is equal to 0, or the brackets term is equal to 0:

This is how we get our two answers, the answers that make these equations true. One answer is obviously x = 0. The other answer we can calculate:

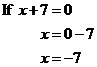
So our overall answer is that x can equal either 0, or –7:

Sometimes you’ll get a question which is already factorised, like this one:

Because their product is equal to zero, one of the brackets must equal zero, so we have two very simple equations to solve in order to find the two possible values of a: