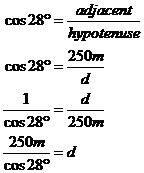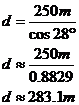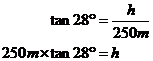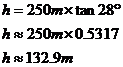Finding angle question

Find θ to the nearest degree:

Solution

If the diagram is roughly to scale, we can make an initial guess at what θ is – let’s say it’s about 40°.  Now, to check whether that’s a good guess, we can use a trigonometric ratio.  But which one to use?  Well, relative to the θ angle, the ‘5’ side is the adjacent side, and the ‘6’ side is the hypotenuse.  So we want the cos ratio:

So what we are trying to do is find a value of θ that will make this equation true.  Now, we’ve guessed that θ is 40°.  We can use our calculator to work out what cos of 40° is:

So our guess of 40° gives us an answer of 0.7660, which is smaller than 0.8333.  Let’s try increasing our guess for θ to 41°:

Uh-oh!  0.7547 is even further away from 0.8333, so perhaps we should be reducing our guess for θ, down to 39°:

Aha!  We’re getting closer to 0.8333 now, so we should continue decreasing our angle.  Now, once you get used to this sort of thing, you may be able to jump around a little with your guesses.  For instance, going from cos 40° to cos 39°, the result only changed from 0.7660 to 0.7771, and we want to get all the way to 0.8333.  So let’s try skipping a few degrees, perhaps go all the way down to 35°:

That’s a lot closer to 0.8333, but we’re still a bit short.  So let’s drop another 2

degrees:

Now, 0.8387 is larger than 0.8333, so we’ve probably gone a bit too far.  Let’s

go back to 34°:

So the cosine of 33° is 0.8387, which is larger than 0.8333, and the cosine of

34° is 0.8290, which is smaller than 0.8333.  So the actual angle we’re looking for must be somewhere between 33° and 34°. The question asked for the angle to the nearest degree, so we’re going to have to pick one of them.  One approximate way to pick the closer angle is to see which of their cosines is closer to 0.8333:

cos 33°:

cos 34°:

So the result of cos 34° is a smaller distance from what we want – 0.8333, so we’ll use it as our answer – θ = 34°. There is a much faster way to do this question using the inverse cosine function on your calculator, which is covered later. However, it’s good to have an idea of how to approach a problem like this using trial and error.

River rowing question

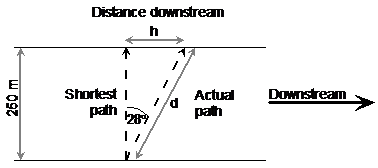
Bobby rows his boat across a wide river.  He aims straight at the other bank, but because of the current, his actual path is a straight line 28° away from the shortest path across the river.  The river is 250 metres wide.  How far did Bobby actually travel?  How much further downstream is he then if there had been no current?

Solution

First up, let’s draw a diagram.  We need a river, 250 metres wide.  We need to draw Bobby’s path across the river, which is a straight line, but 28° away from what the shortest path across the river is.  So we could also draw this shortest possible path in the diagram as well.

So in this diagram I have drawn the river by drawing two parallel straight lines horizontally – these lines represent the banks (sides) of the river.  In between them is the water, where I’ve drawn the two paths across the river – the shortest possible path and the path that Bobby actually took.  I’ve labelled these paths as well.

I’ve put numerical information from the question into the diagram – the river is 250 metres wide, and Bobby’s path is 28° off the shortest path direction.  I’ve also labelled the things that we want to try and find.  The distance Bobby actually travelled is labelled using a ‘d’.  The distance further downstream between where he would have been had he gone straight across the river, and where he did go because of the current, is labelled using a ‘h’.  Downstream is the direction that the current is flowing in.

So we’ve got a diagram, now we need to find some answers.  The central part of the diagram you should quickly realise is just a right-angled triangle.  And we know one of the angles in it – 28°, and also one of the side lengths – 250 metres.  This means we can use trigonometry to find the lengths of the other two sides – which happen to be the two things we’re trying to find out.

First up, let’s find the length of ‘d’.  Relative to the angle 28°, I have labelled which sides are the adjacent, opposite and hypotenuse.  To find ‘d’, we want a trigonometric ratio that involves both the unknown ‘d’, and the known side which is 250 metres long.  These are the hypotenuse and adjacent sides, so we want to use cos:

After a bit of rearranging, all we need to do now is use our calculator to work out what cos 28° is, and find d:

Looking at the diagram, this distance seems to make sense.  Let’s move on to finding ‘h’.

Once again we want a trigonometric ratio that involves the unknown side ‘h’ and the known 250 metre side (we use the 250 metre side instead of the 283.1 metre side because it’s an original value, not one we just calculated).  The two sides are the opposite and the adjacent, so we need tan:

Now we just use our calculator:

Notice I’ve used  symbols in the final steps of finding each answer, because once you actually use your calculator to find the value of a trigonometric ratio, the decimal answer you get out is not exact, it’s quite accurate, but not exact.  Also, the final answer is rounded to only one decimal place.