So far, all we’ve done is work out which two sides are involved in each ratio, given a triangle and an angle we’re interested in.  We haven’t done any calculations with actual values yet though.  If we’re given a triangle and told what the side lengths are, we can actually write a ratio with values in it.  Take this triangle for instance:

Now, say we want to write the tangent of the 30° angle.  Using SOH CAH TOA, we want the ‘TOA’ bit, which tells us that tangent is the (O)pposite side divided by the (A)djacent side.  The opposite side to the 30° angle is the side of length 4.  The adjacent side is the side touching the 30° angle which is not the hypotenuse, so it is the side of length 6.9.  But now we have actual real numbers we can write in our ratio:

                                      

Perhaps we’re interested in the cosine of the 60° angle?  Well, this means we want the “CAH” part – (C)osine is the (A)djacent side divided by the (H)ypotenuse:

                                        

Using trigonometry to work out side lengths

Trigonometry becomes very useful when you have a right-angled triangle which you know some side lengths and angles for.  You can use these three ratios – sin, cos and tan – to help you find the unknown side lengths and unknown angles.  Take this right-angled triangle as an example:

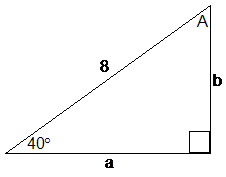
There are two unknown side lengths in this triangle, and one unknown angle.  I’ve labelled the three unknowns using letters, using a capital letter for the angle, and lowercase letters for the sides.  Often when you have an unknown angle and an unknown side opposite it, you use the same letter for each – a capital for the angle and a lowercase letter for the side opposite it.

The unknown angle is easy to work out – since we know angles add up to 180° inside a triangle, and we’ve already got a 40° and 90° angle, the unknown angle must be 50°.

The two unknown side lengths though are harder to calculate.  We can’t use Pythagoras’ Theorem because we only know one side length, and we’d need to know two to use Pythagoras’ Theorem.  What we can use is our trigonometric ratios, but we’re going to need a calculator to do it.

Your calculator can give you the answer to any trigonometric ratio you want.  Say we want to find how long side ‘a’ is.  What we can do is write a trigonometric ratio which has ‘a’ in it.  To do this, we’re going to have to pick one of the angles (apart from the right angle) in the triangle.  Let’s pick the 40° angle.

Now, we only know one side length – we know the hypotenuse is 8 long.  What we want is a trigonometric ratio that involves both the side we’re trying to work out (side a) and the side we already know.

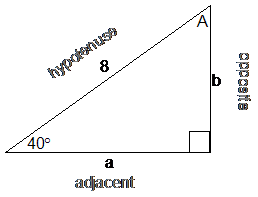
So since we’re using the 40° angle, we want a ratio which involves the adjacent side and the hypotenuse.  Let’s go through our SOH CAH TOA:

(S)in is the (O)pposite over the (H)ypotenuse, so it won’t work.

(C)os is the (A)djacent over the (H)ypotenuse – bingo, that’s what we want.

So we can write a trigonometric ratio using cosine:

                                            

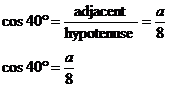
So we have two unknowns in our equation – ‘cos 40°’ and ‘a’.  This is where our calculator comes in handy.  Your calculator can give you the value of any trigonometric ratio you want.  So if we want to find out what cos 40° is equal to, we just type it into our calculator:

Trigonometry on the calculator
First we need to specify which of the three trig ratios we’re using.  In this case it’s cosine, so press the  button. Next we need to tell the calculator what angle we want the ratio for.  In this case, it’s 40°.  So type in ‘40’. Press the  button and you should get an answer of 0.766044443 on your screen.	First we need to tell the calculator what angle we want the trigonometric ratio for.  In this case, it’s 40°, so just type in ‘40’. Now we need to tell the calculator which trigonometric ratio we’re using.  In this case, it’s cosine, so press the  button. You should get an answer of 0.766044443 on your screen.

So because we know what cos 40° is equal to, we can rewrite our equation, and solve it, since we’ve only got one unknown – ‘a’:

                                          

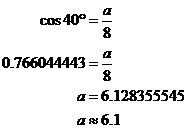
So we’ve managed to find the length of one of the unknown sides.  It’s generally a good idea to have a diagram which is roughly to scale – that way you can check whether the side lengths you calculate make sense.  In this case, side ‘a’ seems to be shorter than the hypotenuse, but not by too much – it’s more than half as long.  So we’d expect an answer below 8, but above 4 – 6.1 sounds quite reasonable.

We can work out the length of the other unknown side ‘b’ as well.  We can use either the 40° angle or the 50° angle. Let’s use the 40° one again.  Now, once again, we want our ratio to have both our unknown side in it and also a known side.

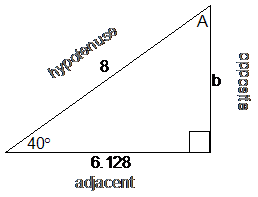
Here’s the updated diagram.  As you can see, we now know all the side lengths except for the ‘b’ side.  Which ratios could we use – SOH CAH TOA?

·         Sin 40° is the ratio of the opposite side over the hypotenuse – this involves our unknown side and a known side, so this would be OK.

·         Cos 40° is the ratio of the adjacent side over the hypotenuse – this isn’t any use, because this ratio doesn’t involve the side we’re trying to find the length of – side ‘b’.  So we can’t use cos 40°.

·         Tan 40° is the ratio of the opposite side over the hypotenuse – this involves our unknown side and a known side, so it’s OK too.

So we’ve got two options – sin or tan.  Now, it’s always better to use original values given in the question in your calculations if possible, instead of values you’ve calculated as you’ve worked through it.

So it’s best if we use the sin ratio:

                                             

Now, rather than working out what sin 40° is straightaway, let’s rearrange this equation so we get it in the form “b = something…”:

                                                  

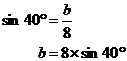
Now once we work out sin 40° we can immediately multiply it by 8 to get our answer for ‘b’, rather than having to write it down and type it back into our calculator, which is a lot more error prone.  Now we just calculate what sin 40° is and find ‘b’:

                                                   

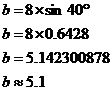
From the diagram ‘b’ looks like it’s around the same length as ‘a’, but perhaps a little bit shorter – 5.1 makes sense as an answer.

Using Pythagoras’ Theorem to check your triangle side lengths

If you’ve worked out all the side lengths of a right-angled triangle using trigonometry, there’s one quick check you can do to see if your answers make sense.  All you need to do is check whether Pythagoras’ Theorem holds true for your triangle and its side lengths.  We can do it for the triangle we worked with in the last section:

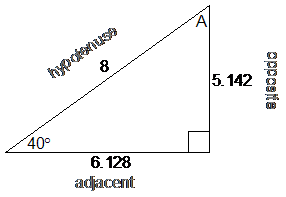
So Pythagoras’ Theorem is that the square of the hypotenuse is equal to the sum of the squares of the other two sides:      

                                 

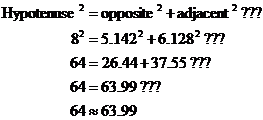
So Pythagoras’ Theorem works for the side lengths we’ve calculated, which is a good sign for our answers being right.

Deciding whether you have enough information

Now, even though trigonometry allows you to find side lengths which you couldn’t solve with just Pythagoras’ Theorem, there’s a limit to what even it can do.  In order to be able to work out what all the side lengths and angles in a right-angled triangle are, you need to know at least the following:

·         One of the angles in the triangle apart from the right angle

·         One of the side lengths

So if you’ve just got one angle, you’ve got no chance.  Same for if you only know the length of one side – no chance.  But remember, sometimes even though the diagram doesn’t have enough information in it, there might be extra information written in the question.