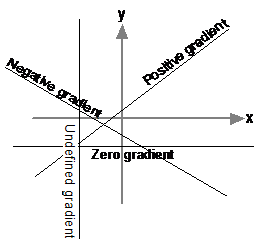
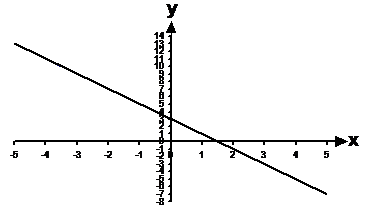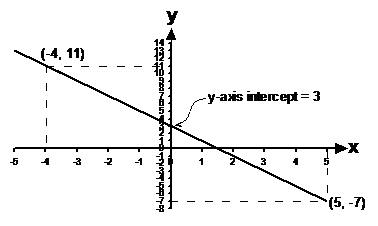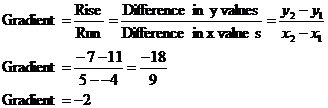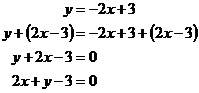A straight line which slopes upwards going from left to right has a positive gradient.  A straight line which slopes downwards going from left to right has a negative gradient.  A straight line that is exactly horizontal has a gradient of 0.  A vertical line has an undefined gradient.

‘Positive’ and ‘negative’ are qualitative descriptions – they describe something without using exact numbers.  There are also quantitative ways to describe the gradient of a line as well.  Describing a straight line as having a ‘gradient of +2.3’ is a quantitative description.

The gradient describes how much a straight line goes upwards or downwards if you travel 1 unit to the right along the horizontal.  Here’s a typical straight line graph:

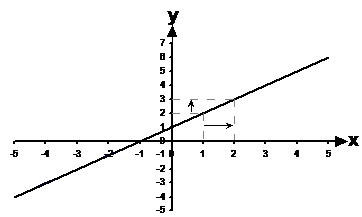
Now to work out the gradient, you can start at any point on the line.  I’ve chosen the point x = 1, y = 2.  Now, move one unit to the right, along the horizontal axis (in other words, in the direction of the x-axis).  How much has our line gone up or down?  Well, in this case, the line has gone up, and it’s gone up from y = 2 to y = 3, a total increase of 1.  So the gradient of this straight line is 1.

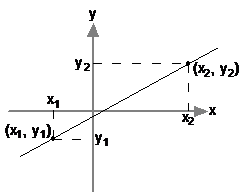
The gradient can also be described as the ratio of the ‘rise’ over the ‘run’.  Rise is how much your line goes up or down in the vertical (y) direction, and ‘run’ is how far you travel in the horizontal (x) direction.  In the last graph, the run was ‘1’, since we went from x = 1 to x = 2.  The rise was ‘1’ as well, since we went from y = 2 to y = 3. Here is a general way of working out the gradient:

                        

This gives us a more flexible way of calculating gradients.  All we need are two points on the line, preferably a fair way apart, like in the diagram above.

For positive gradients, the larger the gradient, the steeper the line slopes upwards.  For negative gradients, the more negative the gradient, the steeper the line slopes downwards.

Graph to gradient-intercept form

A common question in this topic gives you a graph with some information on it, and asks you to write the equation for the straight line.  Usually, it will ask for the equation in the gradient-intercept form:

                                                         

Now, the ‘m’ and the ‘c’ in this equation have special meanings:

·         ‘m’ is the gradient of the straight line

·         ‘c’ is the y-axis intercept of the straight line

This means that you only need to get these two pieces of information from the graph in order to write the equation.  Sometimes you might get asked to write the equation in a different form.  Not to worry, write it first in gradient-intercept form and then rearrange it into whatever form you’re asked for.

Straight line graph equation question

Write the equation for this straight line graph, in the general form.

Solution

Well, the plan is to write the equation first in gradient-intercept form, and then to convert it into the general linear equation form.  To write it in gradient-intercept form, we need to know the gradient and the y-axis intercept.  The intercept’s easy, we can read it straight off the graph – the line intercepts the y-axis at y = 3.  The gradient we’ll need to calculate, we can pick two points on the line a fair way apart and use our rise over run calculation:                          So we know that m = –2 and c = 3, so we can write our equation in gradient-intercept form:                                                          We want it in general form, which is with everything on one side and only a ‘0’ on the other, so we need to rearrange it a bit:                                           This is now in the general form .