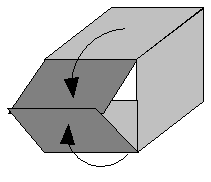
The net of a solid shape is the flat shape that you can fold together to get the solid shape. If you take apart a cardboard box or a shoebox and lay it out flat, what you have is the net for the box. One of the simplest nets is for a cube, it looks like this:

Sponsored Links
One of the interesting things about nets is that there are often multiple different nets that all fold together to give the same shape. For instance, this net will also fold together to form a cube:
The main things you need to be able to do with nets are:
· Name the solid shape based on a net diagram
· Draw the solid shape based on a net diagram
· Draw a net based on the diagram of a solid shape
· Tell whether it is possible to form a solid shape using a certain net
Pyramid nets generally look something like this:
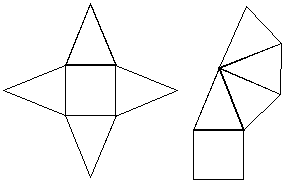
To tell if it’s the net of a pyramid, what you’re looking for is a base shape, of which there is only one, and then as many identical triangles as there are sides of the base shape.
Here’s a net of a triangular prism:
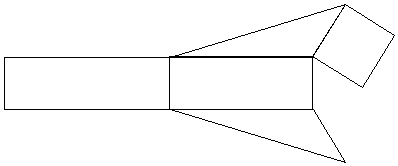
If you’re looking for the net of a prism, you need to find two identical shapes that form the two prism bases. All the other shapes need to be parallelograms.
You need to be able to visualise in your head how to deconstruct a solid shape into a net, and also vice versa – how to construct a solid shape from a net. The best way to get good at this is to make some nets yourself and practise putting them together and then taking them apart. For a simple shape like a rectangular prism, experiment with all the different possible nets you can use to form the solid shape – there are lots!
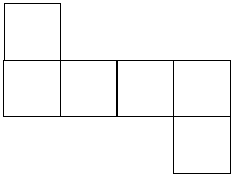
Once you’ve practised a bit you should be able to draw several different nets for forming each of the typical solid shapes. You should also be able to spot ‘impossible’ nets which you can’t actually form a solid shape from, like this one:
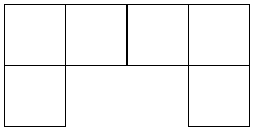
Although this may look like just the net for a cube, if you try and fold a cube from it you’ll find it’s impossible to do it. This is because once you’ve folded the row of four squares up, the two remaining sides actually overlap each other instead of being on opposite sides of the cube like we need: