Cyclic quadrilaterals
Triangles aren’t the only shapes that you can fit inside circles. You can also fit four-sided shapes inside a circle – quadrilaterals. Not all quadrilaterals will have all four corners touching the circumference of the circle. Quadrilaterals that do however are known as cyclic quadrilaterals.

Sponsored Links
Cyclic quadrilaterals have a special property – opposite angles are supplementary (add to 180°). To prove this, you need to split the quadrilateral up into 4 triangles, by drawing lines from the circle centre to the corners. Because each line we draw is a radius of the circle, this means that the four triangles we’ve formed are all isosceles triangles. This means that the outer angles in each triangle are the same, so we can label them to show this:
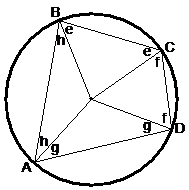
Now, we know that the sum of the interior angles of a quadrilateral is 360°. So we can write down an equation:
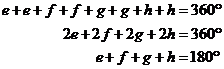
Notice that ‘e + f’ together make up the angle in one corner of the quadrilateral, and that ‘g + h’ make up the angle in the opposite corner of the quadrilateral. We can rearrange the equation to show this a bit more clearly:
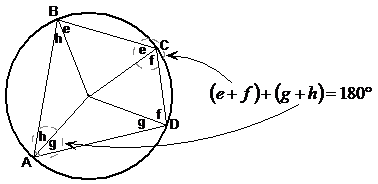
Now what about the other two corners – we need to prove that their angles add up to 180° as well. One corner is made up of ‘h’ and ‘e’, and the other corner is made up of ‘f’ and ‘g’. We can do this by rearranging the equation in a slightly different way:
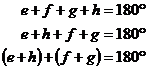
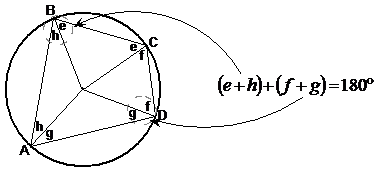
This shows that the opposite angles of a cyclic quadrilateral are supplementary.
Can you draw a circle through the vertices of a quadrilateral?
One type of question will give you a quadrilateral, with angles marked in it, and ask you whether it is possible to draw a circle through all of its vertices (corners). In other words they’re asking whether it’s a cyclic quadrilateral or not. All you have to do is check whether both sets of opposite angles are supplementary or not. If they are, it is possible. If not, it’s not possible. Pretty simple really.
Rectangles are cyclic quadrilaterals because all the angles inside a rectangle are 90°. Opposite angles obviously add up to 180° then. A square is a cyclic quadrilateral too for the same reason.
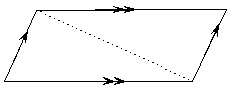
Parallelograms and trapeziums are not cyclic quadrilaterals because their opposite angles don’t add to 180°. The only exception for parallelograms is when they are a rectangle. In a parallelogram, the adjacent angles are supplementary, rather than the opposite angles:

However parallelograms do have another neat property: you can get two congruent shapes by drawing a diagonal line between either of the two opposite corners in a parallelogram. For instance, the two triangles formed by drawing the dotted line in this parallelogram are congruent shapes: