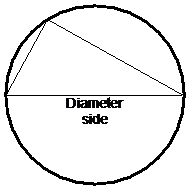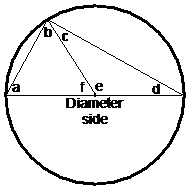Shapes inside circles
Here’s a circle:

Sponsored Links
Now there are some other terms you need to know when you’re dealing with circles.
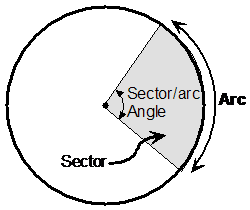
Chords and segments
A chord is a straight line that joins any two points on the boundary of a circle. When you draw a chord, you divide the circle into two areas. These areas are called segments. The smaller area is called a minor segment. The larger area is called a major segment.

Arcs
We already know that sectors are like wedges of a pie or cake. Well, an arc is the part of the circle’s circumference taken up by the sector:
We know that the circumference of a circle is just two pi multiplied by the radius of the circle:
![]()
The length of an arc is always going to be some fraction of the circumference. Say we had an arc with an angle of 180°. This would mean the arc would stretch halfway around the circle – so the arc’s length would be half the circumference. The arc’s angle, 180°, is also half the total angle you need to rotate through to get a circle – 360°. This is no co-incidence – the fraction that the arc’s angle is of 360° is the same as the fraction that the arc’s length is of the circumference of the circle:
![]()
Triangles inside circles
Sometimes you’ll get questions which have triangles, sometimes more than one, drawn inside a circle. You’ll usually get supplied with some information about the angles and side lengths. Also you might get information telling you that a corner of a triangle is located at the centre of the circle for instance.
Usually these questions will ask you to find another angle in the diagram, or the length of a side. Alternatively they might ask you to name whether the triangle is an acute triangle or an obtuse triangle, or perhaps to count how many isosceles triangles there are in the diagram. Here’s an example diagram:

There are a few things that will help you solve a question like this. First up, remember that the sum of the three interior angles of a triangle is 180°. Also, any straight line from the centre of the circle to the circle’s circumference is a radius of the circle. Make sure what you think is the centre of the circle is clearly said in the question. Some questions might try and trick you by drawing lines from what seems to be the centre of the circle, but not specifically say anywhere that it is the centre. What you’re looking for is a statement like in the diagram like, “A is the circle centre.”
In this diagram, lines AD, AC and AB are all the same identical length, since they are all circle radii (‘radii’ is the plural form of ‘radius’). This helps you if you are asked how many isosceles triangles there are in the circle – an isosceles triangle has two sides exactly the same length. Triangle ACD has two sides the same length – AD and AC. Triangle ABC has two sides the same length as well – AC and AB. So there are two isosceles triangles in the circle.
Triangles with a circle diameter as one side
A triangle drawn inside a circle with one side as the diameter of the circle has a special property. The angle in the triangle opposite the diameter side is always 90°:
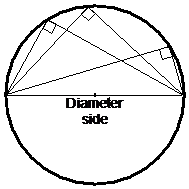
There’s a pretty easy way to prove this is always true. All you need to do is split a triangle in two by drawing another radius from the origin to the corner opposite the diameter side. Then you just label all the angles, and write some equations about what the sum of angles inside the triangles must be:
|
First take a triangle inside the circle…
|
…and add a line from the circle centre to the corner opposite the diameter side
|
Now, we know that the interior angles inside any triangle add up to 180°. So we can straight away write two equations, one for each triangle:
![]()
We are trying to prove that the angle of the original triangle opposite the diameter side is 90°. In our new diagram, this angle is made up of ‘b’ and ‘c’. So we’re trying to prove that b + c = 90°.
At the moment, we have two equations, but we have six unknowns – a, b, c, d, e, and f. We need more information – as in more equations.
There is a straight angle at the centre of the circle – ‘e’ and ‘f’ together make up a straight angle, or 180°. So that’s another equation we can write:
![]()
Now, what types of triangles are these? Well, both have two sides the same length, so they are isosceles triangles. Another property of isosceles triangles is that they have two angles exactly the same size. The identical angles are opposite the corner where the two identical length sides meet. So in the left triangle, angles ‘a’ and ‘b’ are the same. In the right triangle, angles ‘c’ and ‘d’ are the same. So that’s two more equations:
![]()
We now have a total of five equations, but we’ve still got six unknowns. So we don’t have enough information to work out the value of all the unknowns. However, because we’ve only got one less equation than unknown (5 versus 6), we should be able to work out some simple relationships, like ‘a + c = …’ or ‘f – b = …’ What we’re interested in is what ‘b + c’ equals.
If we start with these two equations:
![]()
We can add them together to get:
![]()
Now, we know that a = b and c = d. All we’re interested in is ‘b’ and ‘c’, we want to get rid of all the other variables. So what we can try and do is instead of writing ‘a’s in the equation, we can write ‘b’s, and instead of ‘d’s in the equation we can write ‘c’s:
![]()
We’re interested in ‘b’ + ‘c’, so we can rearrange the equation so that only terms with ‘b’ or ‘c’ in them are on the left hand side.:
![]()
Okay, so now all we’ve got to do is get rid of the ‘f’ and
the ‘e’. There’s another equation we haven’t used yet – the ![]() one. If we
rewrite our current equation a little:
one. If we
rewrite our current equation a little:
![]()
Now instead of ‘e + f’, we can write 180°:
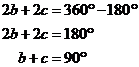
The last step was just to divide both sides by 2. Now we’ve got an equation saying that b and c together make up 90°. This is our proof! Notice that this proof applies for any triangle inside a circle where one side is the diameter, and the corner opposite the diameter touches the circumference of the circle.