Compound as a verb means to combine or add to.  When you talk about compound interest, we’re talking about using interest earned to add to the principal amount.  Here’s a simple example:

Say we start with $2000, and we’re earning 10% interest per year.  Now if this was simple interest, we’d earn 10% of $2000 in the first year, which is $200.  In the second year we’d also earn 10% of $2000, which is another $200.  This would keep going on for ever.  Notice how the amount of interest I earn each year is calculated using the initial principal amount of $2000.

Now, if we were earning 10% compound interest per year, what happens is that the interest we earn each year is added to the principal amount.  So in the first year, we’d earn 10% of $2000, which is $200.  This amount would be added to the principal, so that at the start of the second year, we had a principal of $2200.  During the second year, the amount of interest we earned would be calculated using this new principal amount of $2200.  So in the second year, we’d earn 10% of $2200 in interest, or $220.  Notice how we’ve earned more interest in the second year!

Here’s a comparison of simple interest and compound interest next to each other over a period of 4 years, for a principal of $2000 and an interest rate of 10%:

Using compound interest, you earn more interest on your money.  This is because the interest earned each year is added to the principal, so each time you calculate interest, you’re taking 10% of an ever increasing principal amount.

Compound frequency

When you work with compound interest, there’s another thing you need to know, the compound frequency.  This is how often the interest is calculated and added to the principal.  The higher the compound frequency, the more interest you earn in any period of time.  To show the difference between different compound frequencies, compare an investment of $1000 at 10% at a compound frequency of once per year, compared with a compound frequency of four times a year.

Interest calculated once per year

                                   

                               

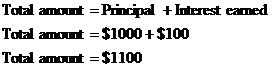
Interest calculated four times per year

So the interest is calculated and added to the principal once every 3 months, since there are 12 months in a year.  Now, remember that the interest rate of 10% is a per annum (per year) rate.  Interest earned over a 3 month period is only one quarter the amount of interest that would have been earned over an entire year.  We can use the simple interest formula, where P is the principal, R is the interest rate as a percentage, and T is the term length with respect to the interest rate.  Because the interest rate is a per year rate, but our time period is only one quarter this length, the term length is 0.25.

                         

                    

                 

                

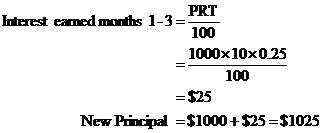
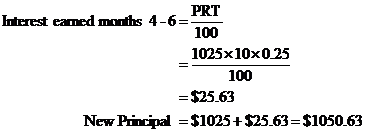
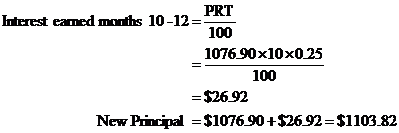
So when the interest is calculated more often, you earn more interest.  In this case it’s only $3.82 more, but it still is more!  The amount extra you earn increases as the compound frequency gets higher – for instance for this same amount and interest rate, if the interest had been calculated every day over a year, then you’d end up with a total of $1105.16.