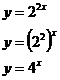Remember how a relationship is all about a rule that relates the value of one variable to another? For instance, a very simple relationship is something like this:
Sponsored Links
This relationship tells us that ‘y’ is always twice as large as x. Exponential relationships are relationships where one of the variables is an exponent. So instead of it being ‘2 multiplied by x’, an exponential relationship might have ‘2 raised to the power x’:
Usually the first thing people do to get a grasp on what exponential relationships are like is draw a graph. Let’s draw one for the relationship above, which is one of the most common exponential ones around. First pick a domain for the values of ‘x’ – let’s use –5 to +5, and use your calculator to find the values of y:
|
x |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
0.03125 |
0.0625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
16 |
32 |
Now to plot it on a graph, the range (values of ‘y’) varies from 0.03 to as large as 32:
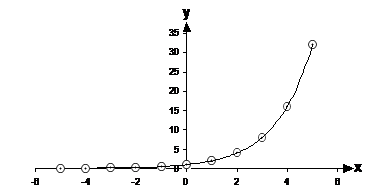
Notice how the slope of the graph for negative values of ‘x’ is almost flat, it’s just a tiny bit of a positive slope upwards. Then as the values of x increase, the slope becomes steeper and steeper. This is a typical line shape for an exponential graph.
Problems extending exponential graphs
It’s very hard to draw an exponential graph over a very wide domain of ‘x’ values. Why is this? Well, look at the graph above and imagine extending it to the left more, for negative values of ‘x’ below ‘–5’. It gets very hard to plot the values accurately because they are so small – 2-10 for instance is 0.00098. It’s just as hard to extend the graph in the other direction though as well. The values of ‘y’ rapidly get very, very large as you go above x = 5. For instance, 210 is 1024. You’re quickly going to run out of space on the page for your y-axis.
This means you have to be very careful when you plan your graphs of exponential relations. Usually, you can only accurately plot an exponential graph over a small number of domain (x) values, otherwise the range (y) values get too small or too large at either end of the graph.
Guessing the exponential relationship from a graph
One type of question will give you a graph of an exponential function, and ask you to calculate what the exponential relationship is. To do this, you just have to remember the general form of an exponential relationship:
Now if you can find the x and y coordinates of a point on the graph, then you know the ‘x’ and ‘y’ values in this equation. All that’s left to find out is the value of a. So we need to rearrange this equation so it’s in the form “a = something…” To do this we have to take the xth root of both sides of the equation:
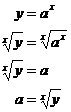
Say we had this graph:
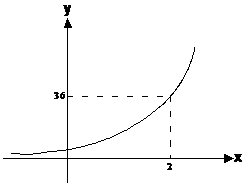
We have numerical information about one point on the graph. We can substitute these values of x and y into our equation to find the overall relationship:
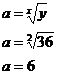
So this means our entire relationship is just:
One thing you should remember when you’re doing this, is
that there is more than one exponential relationship that can work for
this point. For instance, instead of it being , the line could also be represented
by the relationship 
. This relationship also works for
the point shown in the graph:
If x = 2, then:
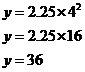
This is still an exponential relationship, because the variable ‘x’ is an exponent. The difference is that this relationship also has a coefficient of ‘2.25’.
You can also have a coefficient in front of the exponent itself, like this:
When you do have a coefficient in front of the exponent, you can always get rid of it by manipulating the index. You’ve just got to remember that a power raised to another power is just like multiplying the two powers together. What we do is the reverse of this – take two powers that are multiplied together and change them into a ‘power to a power’ form:
