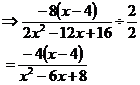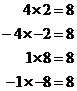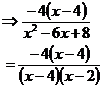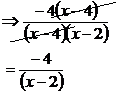Some questions will ask you to simplify a fraction which has pronumerals in it to its simplest form. Sometimes this will be quite easy, such as for this fraction:
![]()
Sponsored Links
The 8 on 4 simplifies to 2 on 1, and the ‘q squared on q’ part simplifies to just ‘q on 1’:
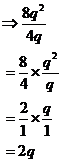
There are much more complicated fractions though which require a bit more thought and fiddling around before you can simplify them. There are a few things you can look for to help you simplify the fraction:
Handy Hint #1 - Simplifying fractions
- Look for common factors that you can divide the top and bottom of the equation by. In the last fraction, ‘4’ and ‘q’ were common factors.
- See if any parts of the top or bottom are perfect squares – if they are you can factorise them.
- See if any parts of the top or bottom are in the ‘difference of two squares’ format – if so you will be able to factorise them.
- See if you can factorise the tops or bottoms in any other way.
Here’s how to use these for a more complicated fraction:
|
Simplify |
|
Solution |
|
First up, are there any common pronumeral factors we can divide the top and bottom by? ‘x’ isn’t a common factor because we can’t divide all the terms on the top and bottom by ‘x’ – for instance, 16 won’t divide by ‘x’. Perhaps there is a number that we can divide both top and bottom by. The largest common factor is going to be limited by the term with the smallest number in front of it, which is the ‘2x2’ on the bottom. So what about ‘2’ as a common factor? We can divide both top and bottom by it: Okay, so now the fraction’s a little bit simpler. Are there any perfect squares on the top or the bottom? Well, the top, when expanded, is just ‘–4x + 16’, which isn’t a perfect square. What about the bottom? Well, let’s assume that x2 is one of the squares, and that ‘8’ is the other squared term. For it to be a perfect square, the other term (–6x) in this trinomial has to be twice the product of the square roots of the two squared terms. So the square root of ‘x2’ is just
‘x’. The square root of ‘8’ is What about looking for a difference of squares? The top could be a difference of two squares – with one square being ‘16’ and the other square being ‘4x’. So we could convert it into a difference of squares expression like this: The square root of 16 is just 4. The square root of ‘4x’ is The difference of squares in factorised form would look like this: This isn’t really any simpler though than just –4(x – 4), so we won’t go this way. The bottom of the fraction obviously isn’t a difference of two squares either because there are three terms in it, instead of only two. This leaves us to try and factorise the top or bottom by any other means possible. The top of the fraction is already pretty much factorised, but what about the bottom? The ‘x2’ term is obtained by multiplying ‘x’ by ‘x’, so we can start with a set of brackets with an ‘x’ in each one: Next up, what pairs of numbers multiply together to give ‘8’? Which of these combinations when multiplied by the ‘x’s in the brackets will give us a total of ‘–6x’? Well, the first combination, 4 and 2, will give us a total of ‘+6x’, which isn’t what we want. But the second combination, –4 and –2, multiply the ‘x’s to give us a total of ‘–6x’, which is what we want. So the bottom of the fraction can be factorised, like this: Let’s rewrite the whole fraction now, using this new factorised bottom: Now we can cancel out a common binomial on the top and bottom, ‘x – 4’: This can’t be simplified any more, so it’s our final answer. Now the first few times you do this it will take you a long time, because there are so many possible ways that the fraction can be simplified. Practice will make you better at recognising perfect squares, the difference of two squares, and quicker at factorising. Also remember that occasionally there will be a question where the fraction can barely be simplified, or not at all even. Don’t spend too much time tearing your hair out on any one question, there is always the possibility the fraction’s already as simple as it can be. |