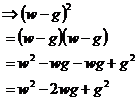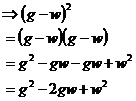There’s an important and very useful type of binomial multiplication which you should be able to recognise. It’s called the ‘difference of two squares’. Here’s an example of it:
Sponsored Links
Now don’t forget that ‘xy’ is exactly the same as ‘yx’, so in fact these are two like terms:
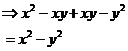
Look how nice and simple our answer is, it’s just
the square of one pronumeral, 
, minus the square of the other
pronumeral, 
.
This is why this is called the difference of two squares – because
you’re subtracting one square () from another square () – you are
actually finding the difference between the two.
Any binomial multiplication which fits this general form can be quickly calculated using knowledge of how the difference of two squares works:
Term A can be any term, as long as it’s in both the first and second set of brackets, same for Term B. The answer to an expression like this is always:
In your final answer, the positive term is always the square of the term which is positive in both brackets. The negative term in your answer is always the square of the term which is positive in one set of brackets and negative in the other. So say we were given this:
First up, the brackets are exactly the same except there’s a negative sign in the second one, so it fits our general ‘difference of two squares’ layout. The positive term in both brackets is the ‘3t’ term, so this will be the positive squared term in our final answer. The ‘2f’ term is positive in one and negative in the other set of brackets, so it will be our negative squared term. Our final answer is:
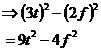
Handy Hint #1 - Mixing up the layout to fool you
A lot of questions will have the layout of the binomial multiplication mixed up to try and confuse you. Take this one for example:
Now up till now we’ve been used to the ‘always’ positive term being at the start of each bracket. In this expression the ‘b’ is always positive, but it’s at the end of the first set of brackets and at the start of the second set of brackets. Not to worry though, we can just rearrange the expression into the normal layout we’re used to:
Notice how the negative sign is now in the first set of brackets, instead of the second as in the earlier examples. This doesn’t matter, if you feel more comfortable with the plus sign being in the first set of brackets, then you can rewrite it again:
Remember to keep an eye out to see whether the expression you’re looking at is indeed a difference of two squares, remembering that you may have to fiddle around with the order a little bit.
Binomial perfect squares
Perfect squares can happen in algebra as well as in number maths. In number maths, we thought of 81 as being the perfect square of 9. In algebra, we can have perfect squares of binomial expressions. For instance, the perfect square of ‘x + y’ is:
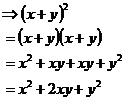
Whenever you square a binomial expression, you’ll always get a standard type of answer. Your answer will always contain these three parts:
· The square of the first term in the brackets, x2 in this case.
· The square of the second term in the brackets, y2 in this case
· Twice the product of the first and second term in the brackets, 2xy in this case.
Only one more thing to be careful of – the sign of the ‘twice the product’ term. If the sign in front of both terms (‘+x’ and ‘+y’ in this case) is positive like in the above example, then the ‘twice the product’ term will be positive. If one of the terms is negative, then the ‘twice the product’ term will be negative. If both terms are negative, then the ‘twice the product’ term will be positive.
So if we had something like this:
Because there’s a negative sign in front of the ‘h’, we know that the ‘twice the product’ term will be negative. So in our final answer, we’ll have:
· The square of the first term in the brackets, g2 in this case.
· The square of the second term in the brackets, h2 in this case
· Twice the product of the first and second term in the brackets, 2gh in this case. But because there’s a negative sign in front of the ‘h’, there will be a negative sign in front of the ‘2gh’, giving –2gh.
Our answer would be:
Factorising perfect squares
Now, if you can recognise an expression which looks like it’s a perfect square of a binomial expression, it makes it easy and quick for you to factorise it. For instance, if we had:
When you look at something like this, you should see that there’s two squared terms – a square of ‘w’ and a square of ‘g’. For this to be a perfect square, there should be one more term. This term should be (wait for it, it’s a bit of a mouthful), twice the product of the square roots of the two squared terms.
Okay, so the square root of w2 is just w. The square root of g2 is just g. Now, the product of them is just g times w, or ‘gw’. Twice this product is just ‘2gw’. Is this what is in the expression – yes! Okay, so now we have to put our expression into factorised form. First up we need a set of brackets which are squared:
Next, we know there will be two terms in the brackets. One term will be the square root of one of the squared terms, and the other term will be the square root of the other squared term:
Last thing we need to do is work out the sign – is it a plus sign or a negative sign between the ‘w’ and the ‘g’. Well, in our expanded expression which we started with, the ‘twice the product’ term is negative:
This means the sign in the brackets will be negative:
One important thing to notice – it doesn’t matter which order you wrote the terms into the bracket, we could have quite easily written it like this:
Check your factorisation! Multiply out the brackets to check you end up with what you started with:
|
|
|
Good stuff. Either way, we get a ‘w2’, a ‘–2wg’ and a ‘g2’ term in our answer, which matches the expression we started with.
You will get more complicated expressions to factorise, things like this:
Same process applies though, first check whether it looks like a perfect square. Well, the first term ‘9x2’ is the square of ‘3x’. The last term ‘16j2’ is the square of ‘4j’. And the middle term looks like it might be the ‘twice the product…’ term. We need to check whether it’s twice the product of the square roots of the two squared terms.
The square roots of the two squared terms are ‘3x’ and ‘4j’. Their product is ‘12xj’. Twice their product is ‘24xj’. This matches with our middle term in the expression, so it looks like it is a perfect square. Now we need to factorise it. First up, we start with a squared set of brackets:
Then we put in the two square roots of the squared terms – ‘3x’ and ‘4j’:
What sign should go inside the brackets? Well, our ‘twice the product…’ term is ‘24xj’, which is positive, so a positive sign should go into the brackets:
Factorising trinomial expressions
A trinomial expression has three terms in it – the ‘tri’ in trinomial means ‘three’. They are the sort of expressions you get when you multiply two binomial expressions together:
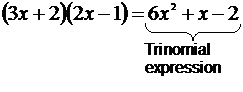
Now for this particular trinomial expression, we know it is possible to factorise it because we got it in the first place by multiplying two binomials by each other. But if you’re just given the trinomial expression, then you don’t know whether you can factorise it or not. There is a simple step by step process though you can follow to try and factorise any trinomial expression. We’ll use the following trinomial expression to work through it:
Now, just to make it easier, here’s how this expression was formed:
It will help with your understanding if you look at how each term in the trinomial was obtained.
· The ‘x2’ term came from multiplying the ‘x’ in each of the brackets.
· The ‘5x’ is actually made up of a ‘3x’ and a ‘2x’ – the terms you get by multiplying the number in each bracket by the ‘x’ in the other brackets.
· The ‘6’ came from the two numbers multiplying each other: 2 × 3 = 6.
Now to factorise this trinomial expression, what you’re really trying to do is the reverse process to multiplying out the brackets. So here’s a step by step process looking at how you can write a factorised expression which will give you each of the terms in the trinomial when you multiply it out.
Find the highest order term in the trinomial. This is the term which has a pronumeral raised to the largest power. In this case, the ‘x2’ term is the highest order term. Now, think about how we can get this term - we need to multiply ‘x’ by ‘x’. This means we’ll need an ‘x’ in each of the brackets:
Look at the term which is only a number in the trinomial (the term which doesn’t have any pronumerals in it). For this trinomial, ‘6’ is the number only term. We need two numbers that multiply together to give ‘6’. There is more than one possible combination of numbers that does this: 1 × 6 = 6, but also 2 × 3 = 6. Which combination you pick depends on step 3.
Look at the term in the trinomial which we haven’t examined yet – the term with both numbers and pronumerals in it. In this case, it’s a ‘5x’ term. How does this term come out of the multiplication? Well, whatever numbers we put into the brackets, they will multiply out the ‘x’s. The sum of these multiplications will have to add up to ‘5x’.
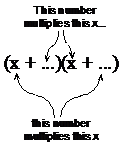
Now what are the options? ‘1’ and ‘6’ are an option, but how many ‘x’s will they give us? We’ll get 6 times ‘x’ plus another 1 times ‘x’ which will give us a total of ‘7x’. We want ‘5x’, so this won’t work. This leaves the other option – ‘2’ and ‘3’. ‘2’ times ‘x’ plus ‘3’ times ‘x’ gives us a total of ‘5x’, which is what we want. So the numbers that need to go into the brackets are ‘2’ and ‘3’:
It’s always good to check that the brackets multiply out to give you the original trinomial expression you were trying to factorise.
A negative sign can make your job a little trickier – something like this perhaps:
So, there’s still an ‘’ term, so we start with:
What numbers multiply together to give –6?
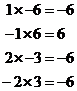
We’ve got four options here. To work out which option to go with, we need to remember that the two numbers will have to multiply out the ‘x’s to give us a total of ‘x’ (not ‘5x’ like in the last example).
1 and –6 multiply out the ‘x’s to give ‘–5x’ – no good.
–1 and 6 multiply out the ‘x’s to give ‘5x’ – no good.
2 and –3 multiply out the ‘x’s to give ‘–x’ – no good.
–2 and 3 multiply out the ‘x’s to give ‘x’ – bingo!
So the two numbers we need are ‘–2’ and ‘3’:
