More algebra

A binomial expression has two terms in it.  A typical binomial expression in algebra might be something like:

                                                            

It’s got two terms – a ‘3x’ term and a ‘5’ term.  Now say I want to multiply this binomial by four – the calculation would just be:

                                                     

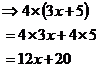
Remember that the 4 multiplies both terms in the bracket.

We can also multiply this binomial by an algebraic pronumeral, such as ‘a’:

                                                     

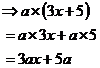
This is pretty easy.  But there are more complicated multiplications we can do.  For instance, we can multiply our binomial by another binomial.  Say we have another binomial, ‘2x – 3’.  Multiplying them together would look like this:

                                                    

Usually, we don’t write the multiplication symbol:

                                                     

To do this multiplication, we just need to remember that each term must multiply every single term in the other set of brackets.  So we must multiply the ‘3x’ term by both the ‘2x’ term and the ‘–3’ term in the other brackets.  Same with the ‘5’ term – we must multiply it by both the ‘2x’ term and the ‘–3’ term.  A lot of people find it easiest to use arrows showing them which multiplications they have to do at first:

                                   

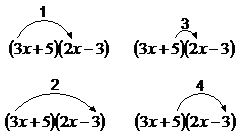
This diagram shows one possible order that you could do the multiplications in.  If we follow the steps in the diagram, the first multiplication is:

                                                       

The second multiplication is:

                                                     

The third multiplication is:

                                                       

The fourth and last multiplication is:

                                                       

So after doing all our multiplications, to get our final answer we just need to add them all together.  Remember, because some of the results we just got were negative, they are going to subtract from our overall answer:

                                                  

Here we’ve put the four results together, but there’s still some simplifying we can do.  The ‘–9x’ and the ‘+10x’ terms are like terms, since they both have ‘x’ in them, so we can simplify them together to get just ‘1x’ or ‘x’:

                                          

Using areas to help visualise binomial multiplication

Calculating the area of a rectangle is really easy – it’s just the length of the rectangle multiplied by the width.  We can ‘convert’ any binomial multiplication into a ‘find the area of a rectangle’ problem.  Say we have to calculate this:

                                                     

What we can do is start with a rectangle:

We can treat each bracket in the multiplication as if it is the length of a side of the rectangle.  For instance, we can say that the length of the rectangle is ‘3x + 2’ and that the width is ‘2x + 4’:

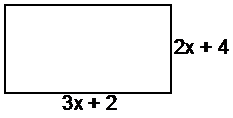
Now notice how each side length has two terms in it.  We can split each side length up into two bits, with each bit the length of one term. We can split up the length side (3x + 2) into two lengths, one ‘3x’ long and one ‘2’ long.  The (2x + 4) side splits up into two lengths, one ‘2x’ long and one ‘4’ long:

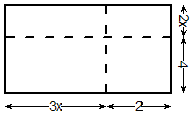
Look at how the rectangle is now split up into four separate areas.  Each of these areas represents one of the multiplications you have to do to find the final answer.  For instance, the area of the top left area is ‘3x’ multiplied by ‘2x’.  This was the first multiplication we did using the method shown in the previous section.  The rectangle does not have to be to scale, because we don’t know how large ‘x’ is.  Notice how the ‘2’ length side and the ‘4’ length side look almost exactly the same length – it doesn’t matter for this method.

To find the product of the two binomials, you just need to find the areas of each of the four sections, and add them together:

                                                

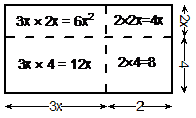
Now, if you had a binomial multiplication like

                                                   

you would need to ignore the ‘negative’ sign in front of the brackets for a little while and just calculate it as if you were calculating .  Then, at the very end, you would need to allow for the negative sign by changing the sign of everything:

                                  

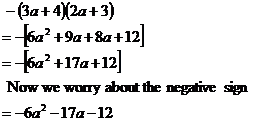
If however, the negative sign is inside the brackets somewhere, then we need to modify our areas approach just a little.  Say we had to calculate:

                                                     

What we’d do is draw the rectangle with the side lengths set as the terms in the brackets:

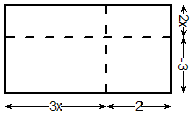
Having a negative term is like taking away area instead of adding it.  What we can do is shade the sections which are ‘positive’ areas.  The ‘negative’ areas, which are any areas which you calculate using the ‘–3’, we’ll leave white:

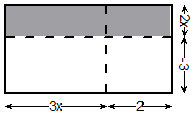
Now we can calculate the areas, remembering that some of them are going to be ‘negative’:

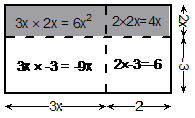
Notice how the areas of the bottom 2 sections are ‘negative’ because calculating them involves the ‘–3’ side.  Now all we do is add up all the section areas to get our final answer:

                                                 

Factorised form and expanded form

You’ll need to know the difference between factorised and expanded form when you’re working with algebraic expressions.  Factorised form for an algebraic expression is when you have the expression written entirely as a product of its factors.  For instance, in an earlier example, this was the factorised form:

                                                     

Expanded form is when you multiply out any brackets in an algebraic expression so you’re just left with terms in a row, like this:

                                                        

Standard types of binomial multiplications

A lot of binomial multiplications have a similar sort of layout.  The most common arrangement has the first term in each set of brackets as like terms, such as these for instance:

                                                    

or

                                                   

In the first one, the ‘3a’ and the ‘a’ are like terms.  In the second expression, the ‘2x’ and the ‘7x’ are like terms.  Now, quite often the second part of each bracket is just a number, something like these perhaps:

                                                      

or

                                                     

There are a few things you can keep in mind when you do binomial multiplication with a typical expression like these.  First of all, your answer after you’ve multiplied it all out will have a term where the pronumeral (the ‘a’ or the ‘x’ for instance) is squared.  Also, you should be able to add like terms and reduce the total number of separate terms.  For instance, let’s try expanding .

We should expect to get a term involving the square of ‘a’.  We should also expect to get some other like terms involving just ‘a’, (not ‘a’ squared).  So when we multiply it out we initially get:

                                                

So at this intermediate stage of our calculation, we have the ‘squared’ term we’re expecting – ‘3a²’, and we also have a couple of like terms – ‘18a’ and ‘4a’.  So we can simplify it a bit more by adding like terms to get:

                                                     

You can also get binomial expressions with more than one pronumeral in them, something like this for instance:

                                                      

These types of multiplications won’t have any like terms in the answer, so you won’t be able to simplify your answer.  You’ll usually be left with four different terms:

                                                  

Notice how none of the terms in our answer are like terms, so we can’t do any more simplification.