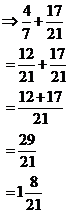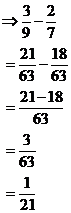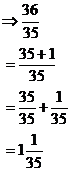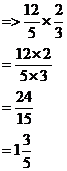You can do all the normal calculations with fractions – addition, subtraction, multiplication and division. There are however some special tricks that are good to know.
Addition with fractions
To add together two fractions, you have to make sure that they have a common denominator. In other words, they must both have the same number on the bottom. This won’t always be the case, so sometimes you have to do some manipulation of the fractions before you can add them together.
Sponsored Links
Say we have the following problem:
|
Add together |
|
Solution |
|
Notice that the fractions do not have the same denominator. Before we can add them together, we will have to make sure they do. So how do we go about doing that? Well, we need to find the lowest common multiple (LCM) of 7 and 21. The LCM is the lowest number that you can get by multiplying both numbers by something. We’ll find the LCM for 7 and 21 to show you what to do: First take one of the numbers – we’ll start with 7. List all the multiples of 7 like this: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70 … Now take the other number and do the same thing: 21, 42, 63, 84, 105 Now find the smallest number that is in both lists. In this case it’s very easy – 21 is the smallest number in both lists. 21 is therefore the lowest common multiple of 7 and 21. Now back to the original fractions. Rewrite both
fractions with 21 as the denominator. For And now we have the first fraction in the form we want – with a denominator of 21. Now let’s look at the second fraction – in this case we don’t have to do anything, it’s already got a denominator of 21. So, let’s rewrite the original sum and calculate it: So addition isn’t very hard at all. Subtraction is quite similar to addition as you’ll see in the next section. |
and 
, we need to multiple the
top and bottom by 3. This is because 7 multiplied by 3 gives 21, which is
what we’re trying to get on the bottom. So:
Subtraction with fractions
When you subtract a fraction from another one, you follow the same process as for addition. Let’s do an example:
|
Solve |
|
Solution |
|
First of all, we need to find the LCM of the denominators. So let’s list the multiples of each number, starting with 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 and also for 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98 Now we have to find the smallest number that is in both lists. After searching for a bit you will find that 63 is the smallest number common to both lists. So 63 is the LCM of 9 and 7. So now we have to convert our original fractions
so that they both have a denominator of 63. For And we do the same thing for Now we can do the calculation: |
. We can work out that to
get 63 on the bottom, we have to multiply 7 by the number 9:
Now, this is the correct answer to the problem.
However, we haven’t done it in the easiest way. If you look back at the
original question, you should notice that one of the fractions isn’t in its
simplest form; 
simplifies
down to 
!
So we should have done this simplification first before we did the rest of the
process. This is something to look for in all problems – make sure you have
made the question as simple as possible before you carry out the calculations.
Multiplication with fractions
Multiplying fractions is in many ways easier than doing addition or subtraction. All you have to do is follow a simple three step process:
Handy Hint #1 - Multiplying with fractions
Multiply the tops of the fraction, in other words the numerators.
Multiply the bottoms of the fractions, in other words the denominators.
Simplify the fraction you get from the multiplication.
So, let’s do an example:
|
Solve |
|
Solution |
|
Now, step 1 is to multiply the tops of the fractions together: Step 2 is to multiply the bottoms of the fractions together: Now we have a single fraction, which is our answer. However, there is still step 3 to consider – we have to write the fraction in its simplest form. The current fraction is an improper fraction – the numerator (top) is bigger than the denominator (bottom). We can change it into a proper fraction by splitting it up into a whole number and a fraction: |
Dividing with fractions
Dividing fractions is only a little bit harder than multiplying. There is only one extra little step, and it’s an easy one. Here are the steps for dividing a fraction:
Handy Hint #2 - Dividing with fractions
Swap the numerator (top) and denominator (bottom) of the fraction doing the dividing.
Multiply the tops of the fraction, in other words the numerators.
Multiply the bottoms of the fractions, in other words the denominators.
Simplify the fraction you get from the multiplication.
The extra step is in bold (the thicker letters). Let’s do an example:
|
Solve |
|
Solution |
|
Step 1 is to swap the top and bottom of one of the fractions (remember only do it to one of them): Note how the 3 and 2 have swapped places. Also look at how we are now multiplying the fractions in the second line, instead of dividing them. Now we just do a normal multiplication: |
Fractions on your calculator
You can use a calculator to make working with fractions a lot easier. What you need to do is find the fraction button on your calculator. There should be two symbols somewhere on your calculator to do with fractions: one which looks like:
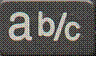
and one that looks like:
Usually, the first symbol is on a button somewhere on your calculator, and the second symbol is above this button, like this:
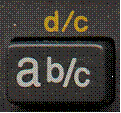or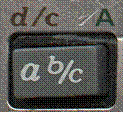 
To show how to use a calculator to do fractions, we’ll do a few example questions:
|
·
Write ·
Write ·
Add ·
Calculate the following: |
|
Solution |
as a proper fraction.
as a percentage.
and 
.
and give the answer as an improper
fraction.|
|
|
|
a) Type in 38. Press the fraction button ( Type in 5. Press the equals sign and you should get 7 b) Type in 16. Press the ‘÷’ button. Type in 17. Press ‘=’. Press the ‘×’ button. Type in 100. Press ‘=’. You should have 94.1176… This is your answer, as a percentage. So, 94.12 %. c) Type in 15. Press the fraction button. Type in 7. Press the ‘+’ button. Type in 18. Press the fraction button. Type in 53. Press the ‘=’ button. You should have 2 d) Type in 37. Press the fraction button. Type in 23. Press the ‘÷’ button. Type in 14. Press the fraction button. Type in 3. Press the ‘=’ button. You should now have Press the ‘–’ button. Type in 16. Press the fraction button. Type in 7. Press the ‘=’ button. You should now have -1 With -1 Now press the Your display should now read: –625
|
a) Type in 38. Press the fraction button ( Type in 5. Press the equals sign and you should get 7 b) Type in 16. Press the ‘÷’ button. Type in 17. Press ‘=’. Press the ‘×’ button. Type in 100. Press ‘=’. You should have 94.1176… This is your answer, as a percentage. So, 94.12 %. c) Type in 15. Press the fraction button. Type in 7. Press the ‘+’ button. Type in 18. Press the fraction button. Type in 53. Press the ‘=’ button. You should have 2 d) Type in 37. Press the fraction button. Type in 23. Press the ‘÷’ button. Type in 14. Press the fraction button. Type in 3. Press the ‘=’ button. You should now have Press the ‘–’ button. Type in 16. Press the fraction button. Type in 7. Press the ‘=’ button. You should now have -1 With -1 Now press the Your display should now read: –625
|
).
3
.
, we’re halfway there.
. Now we have
to change it into an improper fraction. For this we need the 
function. Since this is a secondary
function on most calculators, you need to press the ‘2nd function’
or shift key first, and then press the 
button.
).
function. Since this is a secondary
function on most calculators, you need to press the ‘2nd function’
or shift key first, and then press the 
button.
