In real life you often use or hear about percentages. For example, if you’re at the shops you might see a stereo on sale. On the sign you might see something like:
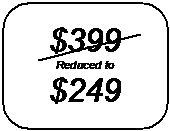
Sponsored Links
In another store, you might see a sign for that same stereo:

So in both stores, the stereo’s normal price is $399.00. However, in one store, this has been reduced to $249.00. In the other store, the stereo’s original price of $399 has been reduced by 30%, but no-one’s written what the new price is. How do you know which store is cheaper? Well you could do it three ways. You could ask the store assistant to work out what 30% off $399.00 is, you could work it out yourself, or you could work out what percentage discount the $249 price worked out to. Let’s try the third option.
So we have an original price, and we have a sale price. To get percentages, you usually divide one number by another, and then turn it into a percentage. To work out what the percentage discount was, we first need to work out what percentage $249 is of $399. We can do this by dividing $249 by $399 and turning it into a percentage, like this:
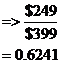
To convert to a percentage, we need to multiply by 100:
![]()
So $249 is about 62% of $399. However, the percentage discount indicates how much percent of the original price has been taken off. Since we’re left with only 62% of the original price, this must mean 38% of the original price was taken off. In mathematical terms:
![]()
So for this problem:
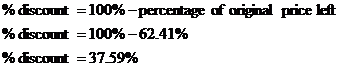
So the discount at the first store is about 38%, which is a larger discount than at the second store.
Don’t be a sucker at clearance sales
Recently I went to one of those clearance sales in a large building where they sell a whole heap of clothing etc… at cheap prices. Now, this particular sale had been advertised all week on the television, with the people on the advertisement shouting out repeatedly, “50% off the original marked price.” So I figured, half-price clothes – that’s a pretty good deal, right? So I went along and had a look, which was when it got interesting…
While I was there, which also happened to be the last day of the sale, an announcement was made over the speaker system. “Final day price cut – take fifty percent off the original price, and then a further forty percent off that”. I heard people all around me going crazy as they did the maths aloud: “Well, that’s fifty percent off the price plus another forty percent off the price…that must mean it’s ninety percent off the original price”. At that point, everyone went nuts and bought as much as they could carry. However, when everyone got to the cash registers, the cost was much more than they had thought, and so they had to return a lot of the stuff. So what went wrong?
Well, these people didn’t listen carefully enough to the announcement, especially the last bit: “Final day price cut – take fifty percent off the original price, and then a further forty percent off that.” Let’s do this with a pretend item which originally cost $100 (this way $1 corresponds to 1%).
So I start with the $100 price. Then I take off 50% off this. 50% of $100 is $50, so I’m left with $50. Everything seems fine so far.
Now, the second part of the announcement – “…and then a further forty percent off that.” “That” refers to the $50 price I’m left with. So this means I take 40% off the $50. If I’m taking off 40%, that means I’m left with 60% of $50:
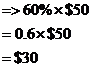
So my final sale price is $30. If you compare this with the original sale price, you’ll see that $30 is 30% of $100. So the overall percentage discount was:
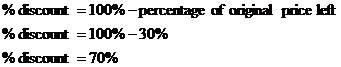
So why did everyone think that the overall discount was 90%? Well, the problem came from the “…and then a further forty percent off that” part of the announcement. The extra 40% discount was not an extra 40% off the original price. It was a further 40% discount on the already discounted price. Only the 50% off part applied to the original price.
This shows how important it is, both in real life, and in school, to make sure you read or listen very carefully, and think about exactly what is meant. In this case, failure to notice a couple of key words – “and then….off that” meant a whole lot of people had a very wrong idea of how much things cost.
Commission
If you ever work as a salesperson, there is a good chance that you will have the opportunity to earn commission on anything you sell. Commission is like an incentive for a salesperson to make lots of sales, because for each sale they make they get paid a small fraction of the sale price. Even though the fraction or percentage may be very small, it can make a big difference to the amount of money you earn over an entire week. Commission becomes very important when you’re selling expensive things, like cars, computers or houses. Even a small percentage of $300,000 is a lot of money!
So if you’re ever offered a job as a salesperson, check out what the salary is like, and whether you get commission. It’s also important to find out what items the commission applies to – sometimes you only earn commission on certain brands. Also, it’s very important to know what the percentage commission is.
So say you’ve just been offered a new job at an electronics store. You get a basic salary of $400 a week (not great for a full time job), but you can also earn commission on any laptop computers you sell. The commission is 2% of the price of the laptop. The manager tells you that the last salesperson managed to sell about 3 laptops a week. You want to know how much money you’d pull in a week based on what he told you. First thing to do is write down a statement saying how much money you could earn a week:
Earnings per week = $400 + Commission
Next thing to do is write down what that commission actually is:
Earnings per week = $400 + 2% on laptop sales
Let’s put in how many laptops we might be selling a week as well:
Earnings per week = $400 + 2% on sales of 3 laptops
So 2% on laptop sales hey? Well this ain’t much use unless you know how much the laptops cost. This is where you make an educated guess. I’m gonna guess that a typical laptop costs $2500. So let’s put that in:
Earnings per week = $400 + 2% on sales of 3 laptops at $2500 a laptop
Now we just need to make it into a mathematical statement and turn some of the words into mathematical symbols and operators. “2% of” becomes a multiplication symbol. The “3 laptops at $2500 a laptop” also becomes a multiplication:
![]()
2% of something is like multiplying it by ![]() or 0.02. So it
becomes:
or 0.02. So it
becomes:
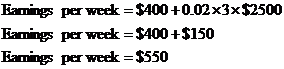
If you do something like this in real life, you’ve got to remember that the only guaranteed money you’ll earn each week is $400. Earning more than this will depend on whether you manage to earn any commission – in this case, this translates to whether you sell any laptops.

