Numbers

Most people can think about simple numbers without having any problems. For instance, most people (except very young kids) could count the number of soccer balls in the picture below and tell me there are three.

Natural, counting and whole numbers

When you count ‘how many’ you are using the natural, counting or whole numbers. For instance the number 3 is a natural, or counting, or whole number. So is 5. So is 1. So is 125.

Some people say that 0 is also a natural, counting or whole number. Ask your teacher what they think – your school may say it is or isn’t. It sort of makes sense – if I opened an empty box and counted the number of apples in it I would get 0! So 0 can be a counting number. –5 (pronounced ‘negative five’) is not a natural, counting or whole number. You can’t count –5 apples.

Negative numbers

Negative numbers are numbers that are smaller than zero. They are a bit hard to understand because you don’t usually deal with negative numbers in real life. For instance, it’s pretty easy to think about a person carrying around 5 apples, but it’s a lot harder or impossible to imagine a person carrying –3 apples around. Negative numbers are very useful though, and not just in maths. Take temperature for instance – if you live in a cold climate, chances are that at night during winter the temperature may drop to below zero – a negative temperature.

Addition using negative numbers

It’s a little tricky at first to do calculations with negative numbers. One of the most confusing things is that a negative or positive sign can have two meanings. Look at the following expression:

If you read that expression out aloud, you’d say something like “five plus four”. In this case, the ‘+’ sign is telling us that we need to add the ‘4’ to the ‘5’. This is the first type of meaning that a plus or negative sign can have – when they are being used as an operator.

Here’s another expression:

In this example, we have both a ‘+’ sign and a ‘–’ sign. The ‘–’ sign in this expression is not an operator. It is just telling us that the 5 is a negative number – ‘negative five’. The ‘+’ sign is still an operator though – it’s telling us to ‘add four’.

When you do any sort of calculations with negative and positive numbers, it sometimes can help to put the numbers and their signs in brackets. Take this expression for example:

We could rewrite this as:

Now, this might seem pointless for such a simple example, but what about something like:

There are lots of different signs here, some are operators, and some are just telling us whether a number is negative or positive. To put brackets around the numbers, just follow this simple procedure:

Handy Hint #1 - Introducing brackets

Put brackets around the first number and any signs in front of it.

For the other numbers:

If a number has only one sign in front of it, put brackets around just the number.

If the number has two signs in front of it, put a bracket around both the number and the sign just in front of it.

Let’s use this procedure to rewrite :

So now we know how to rewrite the numbers. We’ve just got to work out how to do the calculations. To do this, we need a few simple rules:

For addition and subtraction

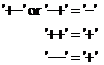
For multiplication and division

· Positive ‘×’ or ‘÷’ positive = positive

· Positive ‘×’ or ‘÷’ negative = negative

· Negative ‘×’ or ‘÷’ positive = negative

· Negative ‘×’ or ‘÷’ negative = positive

Here’s another way of remembering how this all works which I find easier to remember:

· Any operation except for ‘–’ (+, ×, ÷) with two positive numbers always has a positive answer

· Addition with two negative numbers always gives you a negative answer.

· Multiplying or dividing two negative numbers always gives a positive answer

· Multiplying or dividing a negative and positive number always gives you a negative answer.

So if we go back to our example:

So, after we have written our brackets, we realise there are two operations in this expression – a ‘×’ and a ‘+’. Let’s do the ‘×’ operation first:

(–5) × (–3) + ( –2)

So we’re multiplying two negative numbers together: –5 and –3. We know that this always gives a positive number:

= 15 + ( –2)

Now we have a ‘+–’ situation, which we know is like a ‘–’, so we can write:

= 15 – 2

= 13

And that’s how we get our answer: 13. Here’s one more example:

–4 ÷ –2 + –3

First we need to write in our brackets. Remember that the first number always has a bracket around it and any sign before it:

(–4) ÷ (–2) + (–3)

Once we’ve written our brackets in, we can see that we have two operations: ‘÷’ and ‘+’. We do the division first:

(–4) ÷ (–2) + (–3)

We know that any multiplication or division with two negative numbers gives you a positive answer, so we just need to calculate what 4 divided by 2 is:

2 + (–3)

We also know that this ‘+–’ combination is the same as ‘–’, so we can rewrite it:

=2 – 3

= –1

And there’s our answer, –1.

Minus signs outside brackets

You have to be extra careful when you have a minus sign in front of some brackets like this:

–(4 – 2)

Now, this is the same as:

–1(4 – 2)

The –1 is really multiplying everything inside the brackets:

–1 × (4 – 2)

When you multiply any number by ‘–1’, the sign of the number changes. For instance, if I multiply ‘–3’ by ‘–1’, it becomes ‘+3’ – it changes from a negative to a positive number. So if I wanted to get rid of the brackets I’d need to multiply each term inside the brackets by ‘–1’.

So first I get negative one multiplied by positive four:

–1 × 4 = –4

I also get negative one multiplied by negative two:

–1 × –2 = 2

When I put these two bits back together by adding them I get:

–4 + 2

Compare this with the original brackets which were: (4 – 2). The positive four became negative four, and the negative two became positive two – both numbers changed their sign. So:

–(4 – 2)

= –4 + 2

= –2