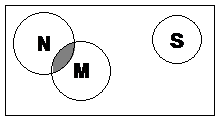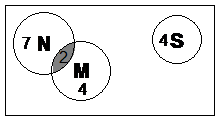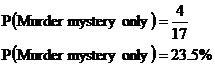Venn diagrams are a way of visualising anything to do with sets, like the sets of outcomes in a probability question. To draw a Venn diagram, we usually start with a rectangle:

Sponsored Links
The area inside this rectangle represents the ‘A’ set in probability – the set containing all the possible outcomes.
Next up, we can draw a shape inside this area representing the set of outcomes where the event E occurs. Because usually not every possible outcome results in E happening, this area is going to be smaller than the rectangle. It’s also usually drawn as a circle shape, something like this:

I’ve labelled the circular area as ‘E’ – telling us that the circular area represents all the possible outcomes that would result in event E occurring.
Now we know that for any event, there is a probability of the event occurring, and a probability of the event not occurring. We also know that these two probabilities together add up to 1, or 100%. The rectangular area represents all possible outcomes in the experiment, so in effect it is like a 100% probability. So if we have an event E taking up a circular area in the space, then the probability of E not happening must be the area outside the circle:
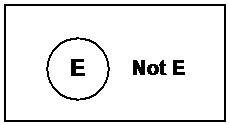
Remember that instead of writing “Not E” we can use
the proper mathematical way of writing it – ![]() .
.
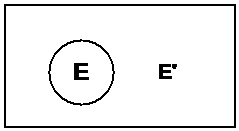
Also remember that the set ![]() complements the set E.
complements the set E. ![]() has all the
events that are not in the set E.
has all the
events that are not in the set E.
Overlapping areas
Sometimes you can have areas that overlap in a Venn diagram. Say we were talking about a class of students. Some students might catch the bus to school. Other students might catch the train. But there would also be a group of students who had to do both to get to school – catch a bus and a train. How would you show this in a Venn diagram? Well, first we start with the rectangular area:

Now, what sets do we have in this question? Well, there are the students who catch the bus only – they form one set, let’s call them ‘B’ for (B)us. Then there’s the group of students who only catch the train – let’s call this set ‘T’ for (T)rain. So we could draw two circular areas within the rectangle representing these two groups:
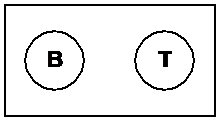
Now what about the students who do both – the ones who catch a bus and a train. Where do they go on the diagram? Well, they definitely belong to the ‘B’ set, since they catch the bus. But they also belong in the ‘T’ set since they catch the train as well. This is where we can use overlapping areas to show that some students catch both the bus and the train:
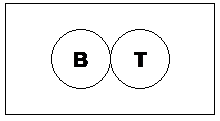

This overlapping area, which is shaded in the diagram, represents the students who belong to both the bus catching and train catching sets of students.

Venn diagram questions
Usually a Venn diagram question will give you information about some sets. You’ll need to draw a Venn diagram that shows this information, and then use the diagram to help you calculate the probabilities of certain things happening.
|
A survey is done on 17 people asking them what shows they watched at night on television. The survey found that of the 17 people, 7 watched the news only, 4 watched a sitcom only, and 6 watched a murder mystery show, of which 2 also watched the news. · Show this information on a Venn diagram. · Calculate the probability of picking a person at random from this survey who only watched the murder mystery show. |
|
Solution |
|
First up, we need to draw the Venn diagram. How many sets are there in this question? There is a set of people who watch the news only. Another set of people watch a sitcom only. Yet another set of people watch a murder mystery. There’s going to be some overlap between the area representing the people who watch the murder show, and the people who watch the news, since some people do both. Let’s call the news set ‘N’, the sitcom set ‘S’ and the murder show set ‘M’. We can start by drawing the rectangle and three circular areas:
It’s good to try and draw the circles so that their size has some relevance to the information in the problem. For instance, 7 people watch the news only but only 4 people watch a sitcom only, so the ‘N’ circle should be quite a bit bigger than the ‘S’ circle. Now, some of the people who watch the murder show also watch the news. This means there should be some overlap between the ‘N’ circle and the ‘M’ circle:
In the question we’re given actual numerical information on how many people there are in each set. We can label the numbers of people in each area on the diagram. First up, what about the news set. It says that 7 people watch the news only. This number belongs in the unshaded part of the ‘N’ area. It also says that 6 people watch the murder mysteries. 2 out of these 6 people also watch the news. So that means 4 people watch only the murder mystery. This number goes in the unshaded part of the ‘M’ circle. The 2 people who watch both belong in the shaded area where the ‘M’ and ‘N’ circles overlap. 4 people watch the sitcom only – so a ‘4’ goes into the ‘S’ circle:
Now we’ve got a completed Venn diagram, we can answer the probability question – what’s the probability of picking a person from the survey who only watches the murder mystery? If we look at our diagram, we can shade the area representing people who only watch the murder mystery:
So 4 out of the 17 people in the survey watch only the murder mystery. Picking a person at random, I have a 4 in 17 chance that I’ll get someone who only watches the murder mystery:
|
‘And’ probabilities
Sometimes you might be asked to work out the probability of event A and event B happening. This is known as an ‘and’ probability. For instance, in the last question, what if we had wanted to know the probability of picking a person at random who watched both the news and the murder mystery?
We’d have to look in the overlap area between the ‘N’ and ‘M’ circles. An ‘and’ probability is always an overlapping area in a Venn diagram:
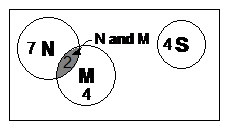
‘Or’ probabilities
When you’re interested in the probability of event A occurring or event B occurring, this is known as an ‘or’ probability. You’re interested in the probability of one or the other happening, or both. Note this is different to what people usually use the word ‘or’ for in everyday life. When you use it in normal life, you usually mean one thing or the other, but not both. In probability though, it means one thing, or the other thing, or both. Try to remember the difference – this is one situation where using everyday commonsense will get it wrong!
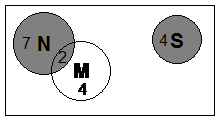
For instance, the area representing the probability of picking someone who watches the news or a sitcom is:
What about the probability of picking someone who watches the news or the murder mystery? Well, the area looks like this:
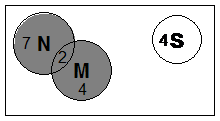
Notice how the overlap area is shaded. This overlap area represents people who watch both the news and the murder mystery, and is included in this ‘or’ probability.