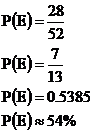I’m going to use a typical question to show you what all the different terms in probability mean.  Here’s the question:

Bob is picking a single  marble out of a bag without looking.  There are 10 marbles in the bag – 4 red ones, 3 blue ones, 2 pink ones and 1 white one.

Trial / experiment

This is all about the thing that is happening – in this case the trial or experiment is Bob picking a marble out of the bag.

Outcome

This is the result of what happens when we do the trial or experiment.  In this case, the outcome of Bob picking a marble is that he will get a marble with a certain colour.

Outcome space

The outcome space is an imaginary space that contains all the possible outcomes that you could get from an experiment.  An outcome in this experiment is Bob picking a marble of a certain colour.  Well, what colours could he get? He could get red, blue, pink and white.  So the outcome space contains four possibilities:

·         Bob could pick a red marble

·         Bob could pick a blue marble

·         Bob could pick a pink marble

·         Bob could pick a white marble

Event

Event is used to describe something that happens which you might be interested in.  For instance, you might be interested in when Bob picks out a blue marble.  The event you’re interested in is, “Bob picking out a blue marble.” 

Probability of an event occurring

Now, we’re usually interested in working out how likely it is that some specific event might happen.  In this example, we might want to work out what the chances of Bob picking out a pink marble were.  The event we’re interested in is, “Bob picking out a pink marble.” 

There is a formal way of writing, “the probability that Bob picks out a pink marble.”  We can use the letter ‘P’ to indicate “probability of”, and then inside some brackets after the ‘P’ write what event we’re calculating the probability for.  The event is usually represented by the letter ‘E’.

                                                             

This simple statement just says something like “The probability (P) of event E occurring.”

Now, back to our example – we’re interested in the probability of Bob picking out a pink marble.  The probability of an event happening is calculated in this way:

                

In this example, since there are two pink marbles in the bag, there are two outcomes where Bob would pick a pink marble.  So ‘2’ goes on the top of the fraction:

                      

What is the total number of outcomes?  Well, there are a total of ten marbles in the bag, of which Bob could pick any one.  This means there is a total of 10 possible outcomes – this number goes on the bottom of the fraction:

                                         

There are lots of ways you can express a probability.  You can leave it in the simplest fractional form:

                                                          

Or you can convert it into a decimal form:

                                                         

Or you can write it as a percentage.  To do this, you take the decimal form and multiply it by 100:

                                                        

Pack of cards probability question

Probability problems involving packs of cards are very common. Some of them can be a little bit tricky, take this one for instance: If you pick a card at random from a normal 52 card pack, what is the chance that you will pick a red card or ace from the pack?

Solution

Okay, so we’ve got our probability formula:                                 Now what is the event we’re interested in?  Well, it’s us picking either a red card or an ace from the pack.  So how many outcomes involve this event? There are 52 cards in a pack.  Half of these cards are red, so that’s 26 events.  What about the aces?  Well, there are four aces in a pack of cards, so that’s another 4 events.  Adding them together, you get 26 + 4 = 30 outcomes which result in the event we’re interested in. WRONG WRONG WRONG!  There’s a problem here.  We are double counting cards – counting a card twice instead of only once.  Think about the 26 red cards in a pack.  Two of the aces in a pack are in these 26 red cards – the ace of diamonds and the ace of hearts.  So once we’ve counted the 26 red cards, we’ve already counted 2 of the aces.  This means that there are only another two outcomes which result in us picking an ace.  So the proper total number of outcomes resulting in the right event is:                                                          Now we just need to find the total number of outcomes possible.  There are 52 cards in the pack, so there are 52 possible outcomes.  So our formula is:                                                        Is this what we expect?  Well, the probability should be at least 50%, because half the cards in the pack are red.  Then there are the two black aces, which should push the probability a bit over 50%.  54% sounds like a very reasonable answer.