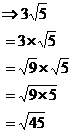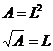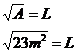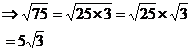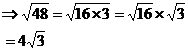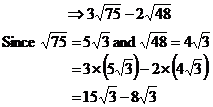Surds

Because so many irrational numbers are ones you get from taking the square root or cubic root of something, there is a special name for these types of numbers – surds. So for instance, the is known as a ‘surd’. Be careful though, only the square roots which are irrational numbers are known as surds. If a square root has an exact decimal answer then it isn’t a surd. So isn’t a surd, because it is a rational number – ‘10’.

What about something like ? Is this a surd?

Typical questions where you answer with a surd

There are quite a few typical situations where you can answer a question using a surd instead of a normal decimal number. Basically, any question where in order to find the answer you need to calculate a square root is one where you might be able to answer with a surd. One example of this is if you are calculating the side length of a square, given the area of the square:

Surd answer question

Find L:

Solution

We know that the area of a square is calculated by squaring its side length:

In this question, we already know the area of the square. We’re interested in what its side length is. This means we need to rearrange the equation into an “L = something…” form. We can do this by taking the square root of both sides of the equation:

We know that the area is 23 square metres. So we can put this into our equation to work out L:

Now, you’ve got two choices here. You can leave your answer in surd form, as . Or you can calculate the decimal answer, which isn’t exact, using your calculator, it should come out something like 4.796 m or thereabouts. Now, some questions will specifically tell you that you should give the answer as either a surd or a decimal answer. If the question doesn’t give you specific instructions, one good way to write your answer is something like this:

First you give the exact surd answer:

Then you give the decimal answer, using a ‘’ symbol, which means, “approximately equal to.” This tells whoever’s reading that you know the decimal answer is only an approximation, and isn’t exact:

Simplifying bits out of square roots

Sometimes you can simplify square roots by looking at the factors of the number being square rooted. If there are duplicate factors in your square rooted number, then you can take one of them out of the square root sign. For instance, if you had this to simplify:

First up, 75 itself isn’t a perfect square, so the decimal answer to this square root isn’t going to be an integer. But how about we look at the factors of 75:

There is one interesting thing about these factors – there are two ‘5’ factors. Now, you can spread out a square root into the square root of each factor multiplied by each other like this:

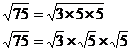
See how I’ve first rewritten the 75 as a product of its factors, and then I’ve split each factor up into its own square root. Now, here’s where another simple thing with square roots is useful:

The square root of something multiplied by itself gives you just the number

So here we have the square root of ‘5’ multiplied by itself. This is the same as just the number ‘5’ with no square root symbol. So we can rewrite this expression like this:

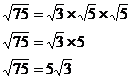
Usually it’s neatest to put the number (in this case ‘5’) in front of the surd, rather than after it. It’s a pretty simple procedure, let’s do it again for . First up, the factors of ‘2000’ are:

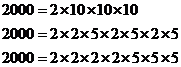
The first line shows the first set of factors I could think of which made up 2000, which was 2 times 10 times 10 times 10. Then I realised that ‘10’ itself was made up of factors and rewrote the ‘10’s as 2 times 5. Then I ordered it so all the ‘2’s and all the ‘5’s were grouped together. Now we can rewrite the original square root:

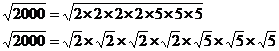
There are lots of simplifications we can make here. First up, there are four ‘’s in total. These four make up two pairs of ‘’s. We’ve also got three ‘’s. These three make up one pair of ‘’s and one single ‘’. To show what we’re doing, we can rewrite the equation using brackets to group the square roots into pairs:

When a square root is multiplied by another identical square root, you’re just left with the number underneath the square root. So our equation becomes a lot simpler:

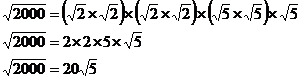
So each pair of square roots multiplied by each other just became the number under the square root. Look at how much simpler the final equation is. This is also a good way to get a quick estimate of what the answer is. All we have to do is estimate what the square root of ‘5’ is, and then multiply it by 20. We know that:

‘5’ is a lot closer to ‘4’ than ‘9’, so the square root of ‘5’ is probably closer to ‘2’ than ‘3’. Let’s say it’s ‘2.2’. Now we just take 20 times this (think of 2 times 2.2, and then multiply that by 10):

The real answer using a calculator is 44.72, so our estimate is pretty good!

Cube root surds

Say you’ve got a cube solid, and you know the volume of it. What if you want to find the side length of the cube?

Well, we know the formula for the volume of a cube, it’s just the cube of its side length:

But in this case, we want to find the length, L, not the volume. So we need to rearrange the equation so that it’s in the form “L = something…”. We can do this by taking the cube root of both sides of the equation:

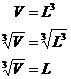
Notice how we’re using a square root symbol, but with a little number written above it to the left. The ‘3’ in this case means we’re taking the third root or cube root of whatever’s under the sign. Now, what happens when you take the cube root of something which itself is cubed? Well, you simply end up with what you started with. For instance:

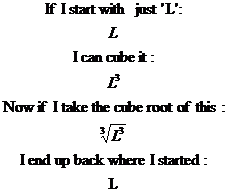
So we have an equation telling us the side length of the cube based on its volume. We can substitute the value of its volume into the equation:

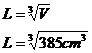
We can also give the answer in inexact decimal form, as well as in the surd form we just calculated:

Remember to use the “approximately equals” sign when you write down your decimal answer.

Roots of numbers smaller and larger than one

It’s good to know about how square roots and cube roots work for numbers that are smaller than one, and also numbers that are larger than one. It’s quite different for each case.

Take a number that is larger than one for instance – 78. If I take the square root of this number, I get a much smaller number:

But if I take the square root of a number that is smaller than one, I end up with a larger number than what I started with. Take ‘0.5’ for instance:

So taking the square root of numbers larger than one gives you a smaller answer, but taking the square roots of numbers smaller than one gives you a larger answer.

If the original number is…	Then the root of it will be…
smaller than 1	larger than the original number
larger than 1	smaller than the original number

This is because there is a critical point around the number one. The square root, or the cube root, or indeed any root of ‘1’ is just ‘1’ again. For a number just smaller than 1, say 0.9, if we multiply it by itself over and over again, the answer just gets smaller and smaller:

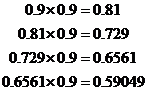
So, taking a root is like going in the reverse direction to multiplying. Going in the reverse direction, the answers get bigger. For instance, the square root of 0.81 is going to be 0.9, because we got . The cube root of 0.729 is going to be 0.9, because we got it by multiplying – . So taking roots of numbers smaller than one gives you an answer bigger than the original number.

It’s the opposite for numbers that are larger than one. For instance, if we multiply the number ‘1.1’ by itself lots of times, the answers get bigger and bigger:

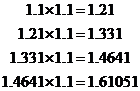
Taking roots is like going in the reverse direction. For instance, the square root of 1.21 is going to equal 1.1, since . The cube root of 1.331 is going to be 1.1, since . So when you take roots of numbers that are larger than 1, your answer is going to be smaller than your original number.

How far away from ‘1’ the number is affects how much smaller or larger the root of it is. For instance, the square root of ‘1.1’ is just 1.049, which isn’t much smaller. But the square root of 2000 is 44.72, which is a lot smaller!

Adding and subtracting surds

In algebra, if you have something like this expression, you know you can add the two terms together because they contain ‘like’ variables – each term has a common variable in it – ‘a’:

Well, you can do the same thing when you’re working with surds. Terms that have the same surd in them can be added to or subtracted from each other. Surds which are the same as each other are known as like surds:

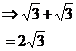
Pretty simple stuff – if I have one ‘square root of three’, and I add it to another ‘square root of three’, I get a total of ‘two square roots of three’. Gets a tiny bit more complicated when the surds have coefficients, but not much:

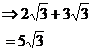
Two lots of plus another three lots of gives you a grand total of five lots of . Easy!

The questions get a bit more complicated again when you get something like this:

Complex surd question

Simplify .

Solution

Now, first up we might panic and go, “Oh my gawd! There are no like surds, so I can’t simplify this expression.” Never fear, even though and are different, I can simplify these surds so that I get some like surds in my expression. To do this, we want to look at the factors of each number. First up, 75:

25 is a perfect square, so I can do the following simplifications:

And for the 48:

‘16’ is a perfect square, so we can simplify this surd as well:

So armed with these simplified surds, we can rewrite our original expression:

Now we’ve got like surds in all of our terms – , so we can do the subtraction:

And we’re left with a nice and simple surd answer.

Multiplying and dividing surds

It’s pretty easy to multiply and divide surds. You can group the numbers all together under one root sign and then do the multiplication or division. For instance, if I had something like:

I can put the ‘3’ and the ‘4’ all under the same square root sign:

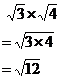
Note that you can’t do this when the surds are different types – you can’t combine a square root surd and a cube root surd for instance:

You can do the same thing for division as well:

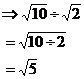
When coefficients come into play, you just deal with them separately:

The coefficients multiply together to give ‘12’, which is the new coefficient in front of the product of the two surds:

So all together:

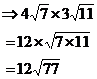
Remember to always check whether you can simplify the expression at all. In this case, there’s no way we can simplify so our answer is in the simplest form already.

Going from a number back to a surd

Sometimes a question might ask you to write a number completely in surd form. For instance, if I had , the question might ask you to write it as a pure surd, which means we have to get rid of the ‘3’ coefficient. How can we do this? Well, we need to move the ‘3’ from in front of the surd and put it inside the surd. We can do this by thinking about what number you’d need to square root to get ‘3’.

If I have any number, then the number I’d have to square root to get it is just that number squared. I have ‘3’, so I can square it:

And now take the square root of it:

and I end up with my original number. So since we know that , we can rewrite our original term: