Pythagoras’ Theorem

Pythagoras was a Greek dude who lived about 2500 years ago.  He did lots of important stuff with mathematics and philosophy, but the thing he is probably most famous for is a simple rule he came up with about right-angled triangles.

His rule simply says that if you take the length of the longest side of a right-angled triangle, and square it, this should equal the sum of the squares of the other two side lengths.  Usually it’s easier to show this with a diagram and an equation:

                                                        

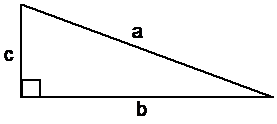
The longest side in a right-angled triangle is called the hypotenuse.  In the diagram, the hypotenuse is side ‘a’. 

Showing Pythagoras’ Theorem working

There’s a visual way you can show how Pythagoras’ Theorem works.  What you can do is take a right-angled triangle, and literally square each of the side lengths – so transform the side into a square with the same side length:

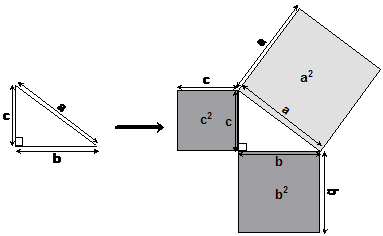
So now each side of the triangle has a square hanging off it, with the square’s side length the same as the side length it’s connected to.  Now according to the theorem, .  We can see whether this is true by dividing the squares up into little squares, and then adding them together to work out the total area of each large square.  So first, we need to divide up the squares into grids made up of little squares, all the same size:

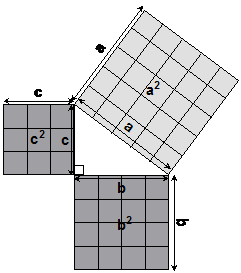
Now, if we add up the number of little squares in the a² area, we get 25 in total.  What about the number of little squares in the b² and c² areas?  Well, the b² area has 16.  The c² area has 9.  Together, there are 25 little squares in the b² and c² areas.  This is the same as in the a² area.  If we put these ‘areas’ we’ve calculated into Pythagoras’ Theorem, we find that the theorem does in fact work.

                                                        

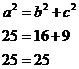
This is a famous way of showing how Pythagoras’ Theorem works, and you should understand it and be able to talk about it in an exam.  You can even draw the triangle and squares on paper, then cut them out and draw the grids, and count them yourself. 

It is easiest if you draw a triangle where the sides are 3 cm, 4 cm and 5 cm long, or any multiple of this, so 6 cm, 8 cm and 10 cm would be OK as well.  If you use a grid size of 1 cm by 1 cm with these side lengths, it means you get a nice whole number of little grid squares inside your big squares, instead of getting little fractions of grid squares.  Counting the number of whole grid squares is a lot easier than trying to add up little bits and pieces of grid squares!

Lot easier to count up complete grid squares…

then to try and add up grid squares when some of them are not ‘whole’.