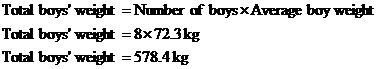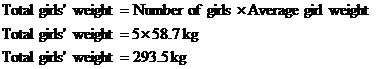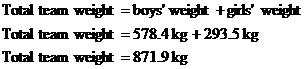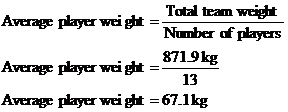The mean and median both give you an idea of what a ‘typical’ value in a set of numbers is.  It’s important to understand how the mean is different to the median.  We can show how they are different by looking at this very simple data set containing the ages of five people:

                                                      12, 12, 13, 13, 28

Okay, first up, let’s find the mean and median of this data set:

First the mean:

                                              

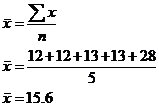
And then the median:

Since there are only a few values, we can skip our normal procedure and just straight away pick the central value – it’s obvious when you’ve only got a few numbers and they’re written in order:

                                              

So the median value is 13, and the mean is 15.6.  There’s quite a significant difference between these two values – which do you think is more representative of the data?  Well, the simple answer is, it depends on how you think the data should be represented!

The mean generally seems to take into account all the values in a data set, which means that one outlier (an outlier is a value that is significantly different to most of the other values) can significantly change the mean.  For this data set, without the ‘28’, the mean or average would have been 12.5.  But because of the ‘28’, the mean got increased all the way up to 15.6.  Notice how 15.6 is larger than all but one of the values in the data set.  So the mean tends to be easily affected by extremely large or small values.

The median is much better at effectively ignoring outliers.  Notice how you could change the 28 to anything you want – you could make it 5,321 (that’s one old person).  The median would remain unchanged:

                                               

Because of the median’s ability to ignore outlying values, it is often regarded as a more robust measure, because it is focused around the middle values and ignores extreme values on either side.

It’s very important to appreciate the difference between the mean and the median.  There are lots of real life situations where it becomes important to understand how they work.

Real estate housing values

Say you’re rich and looking at buying a house in a suburb, but you can’t decide which suburb to buy your house in.  One thing that might influence you is the price of houses in each suburb.  Now there are two statistical measures you could look at – the mean house price, or the median house price.

Traditionally, people have used the mean house price to describe a suburb.  However, in recent times the tendency has been to use the median house price as a guide.  Why has this happened?

Mansions can inflate the average price…

…of a suburb filled with cheap houses.

The big problem with using the mean house price is that one or two mansions in a suburb can significantly increase the value of the mean.  So a suburb filled with $200,000 houses, might have a couple of 10 million dollar mansions in it, which would drive the average price up to say $400,000.  This mean of $400,000 doesn’t represent the typical price of houses in the suburb at all.

The median is a much better measure in this case – the median would be $200,000.  This is due to its abilities to ignore the extremely expensive mansions which are outlying data values.

Averages of averages question

The average weight of the 8 boys in a mixed gender soccer team is 72.3 kg.  The average weight of the 5 girls on the team is 58.7 kg.  What’s the average weight of a player?

Solution

Okay, we’re given two averages, and we need to find an overall average.  One really simple way you might find the answer is by just averaging the two averages like this:                                        This is not the way to find the overall average.  The average weight of a boy on the team is 72.3 kg.  This average is calculated by adding up the weights of all 8 boys on the team, and then dividing by 8.  The average weight of a girl on the team is 58.7 kg.  This average however is calculated by adding up the weights of the 5 girls and then dividing by 5. Each average is calculated using a different number of players.  The average of the boys’ weights is ‘more important’ because it is calculated from more players (8) than the average of the girls’ weight (which is calculated from only 5 players).  The calculation we just did simply added the two averages together and then divided by two.  It treated the two averages as if they were equally important, which they’re not. So, how do you calculate the average weight of a player on the soccer team?  Well, one way is to work out the total weight of the entire team, and divide this by the total number of players on the team.  So if an average boy weighs 72.3 kg, then 8 boys would weight 8 times as much:                    Same sort of thing with the girls – if the average girl on the team weighs 58.7 kg, then 5 of them will weigh 5 times as much:                    So the weight of the entire team put together is just the weight of the boys plus the weight of the girls:                             To get the average player’s weight, we just need to divide this by the total number of players on the team – we’ve got 8 boys and 5 girls, that makes 13 players all up:                               This is the correct average weight of a player on the soccer team.  Notice how it is a little bit larger than the average player weight we calculated using the incorrect “average of two averages” method earlier.  The incorrect method treated the two averages equally, when it should have given more importance to the boys’ average weight (because the boys’ average was calculated from more people than the girls’ average). This is why the correct overall average is slightly larger than the answer we got before – the boys’ weights, which are larger, have had more of an effect on the overall average because there are more boys than girls.