We know that we can use graphs to show statistical information in a meaningful way that people can look at and quickly understand.  Pie charts are useful for showing things like how many votes each candidate in an election is likely to get.  Line charts are great for showing information over time, such as the temperature over an entire year.

There are other situations where graphs aren’t necessarily the best way of presenting the information.  Say you looked at the ages of all the kids in your entire grade.  There might be 100 kids in your grade, and if you listed their ages you might get this:

                        15, 14, 14, 15, 15, 15, 15, 16, 15, 14, 15, 15, 15… and so on

There isn’t really any easy way to graph this information.  We have to resort to other ways of talking about the information. 

There are three main measures used to give people a ‘rough idea’ about all the data.  These three measures are called the mean, median and mode.  To show how each of these measures works, we’ll use the ages of an example class of 13 students:

                                 15, 14, 14, 15, 15, 15, 15, 16, 15, 14, 15, 15, 15

Mean

The mean is the average of all the data.  There is a special symbol for the mean of a set of numbers – it’s an ‘x’ with a horizontal line above it: .  The ‘x’ part represents the bunch of numbers, and the horizontal line means ‘the average of’. 

To find the mean of the ages in our class, you need to add up all the ages, and then divide this sum by the number of kids in the class.  In mathematical terms, this is:

                                      

There’s a special symbol that tells you to add up all the numbers, it’s called a ‘sigma’ symbol.  Instead of writing ‘sum of all the numbers’, you can use the sigma symbol, like this:

                                         

Remember that the ‘x’ just represents all the numbers, and the ‘sigma’ symbol to the left of it just tells you to add up all the numbers represented by ‘x’.

Also, instead of writing, “How many numbers there are,” often in statistics you can represent how many numbers there are by the letter ‘n’.  Think of ‘n’ standing for the (n)umber of numbers.  So we can rewrite our formula for finding the average like this:

                                                          

So, let’s use this formula to find the mean or average age of the kids in the class:

                

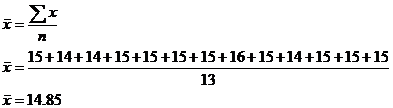
Is this what we expect?  Well, the youngest kids in the class are 14 years old, and the oldest kid is 16 years old.  Most of the kids are 15 years old.  There are more 14 year old kids than there are 16 year old kids, so the average age is probably going to be somewhere around 15 years, but probably a bit less.  14.85 agrees with what we expect.

Median

To get the median of a set of numbers, you first need to write the numbers in order from smallest to largest, or vice versa.  So, let’s order the ages in our class from youngest to oldest:

                                 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16

The median value is the middle value in the list once you’ve ordered them.  To quickly find the median value, follow this procedure:

·         Count up how many values you have in your list

·         If there are an even number of values, divide the number by two.  If there are an odd number of values, add one to the number and then divide it by 2.

·         Take the answer from part 2 and count that many along the list starting from the left. So the leftmost number counts as 1, the next number counts as 2, and so on. If there is an even number of values, the average of the number you arrive at and the number to its right is the median value.  If there an odd number of values, the number you arrive at is the median value.

Let’s use this procedure to find the median of the ages in our class:

                                            There are 13 values in our list.

Since we have an odd number of values, we need to add 1 to it and then divide by 2:

                                                          13 + 1 = 14

                                                           14 ÷ 2 = 7

We need to count 7 numbers across from the left hand number, which count as 1:

                             

Because we have an odd number of values, the median value is just the number we arrived at after counting 7 across.

What if we’d had an even number of ages – say we’d only had 12 in our list (I got rid of one of the ‘15’s):

                                    14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 16

Then the procedure would have been like this:

                                            There are 12 values in our list.

              Since we have an even number of values, we just need to divide it by 2:

                                                           12 ÷ 2 = 6

                    We need to count 6 numbers across from the left hand number:

                              

Because we have an even number of values, we have to look at the average of two values.  They are the number we arrived at after counting 6 across, and the number just to its right – 15 and 15.  The average of 15 and 15 is 15!  So the median is 15.

Mode

The mode is the most commonly occurring number in the entire list.  Usually, there is only one mode in a group of numbers, but sometimes you can get more than one.  Often, the mode is really obvious, but to find it for sure, you need to draw up a table and count how many times each number occurs.  For our class of 13 students, the table would look like this:

                          For ages 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16:

‘15’ is the most commonly occurring age, so 15 is the mode for this set of numbers.  What about if for a different class of students, our table looked like this:

In this case, ages ‘14’ and ‘15’ both occur the same number of times – 6 times each.  This means that we have two modes – 14 and 15.